SCIENZIATI E FILOSOFI (d.C.)

in latino, e di Tâbit ibn Qoran (826-901), precedute da quelle greche di Giamblico di Calcide (250-330), Asclepio di Tralle(VI sev-570) ll Commentario alla Metafisica che ci è stato tramandato sotto il nome di Asclepio di Tralle è in realtà una trascrizione delle lezioni di Ammonio di Ermia (435-517). Figlio di Ermia e di Edesia, e scolaro di Proclo in Atene, fu poi, come il padre, a capo della scuola alessandrina, nella seconda metà del sesto secolo d. C. Ebbe un gran numero di scolari e divenne celebre come matematico ed astronomo, oltre che come espositore e illustratore di testi platonici e aristotelici; e alcuni di tali commenti a scritti di Aristotele sono pervenuti sino a noi, come quelli alle Categorie e al De interpretatione, e i frammenti, editi dal Waitz (nella sua ed. dell’Organum, I, 43), di quello ai Primi analitici: per quanto nessuno d’essi sia certamente conservato nella forma originaria. Suo padre Ermia di Alessandria (410 d.C. circa – 455 d.C. circa) è stato un filosofo neoplatonico egizio di lingua greca,Le scarne notizie sulla vita di Ermia sono tratte dalla Vita di Isidoro del filosofo platonico Damascio,

Giovanni Filopono di Alessandria d’Egitto, (490 circa – 570) è stato un filosofo, teologo, scienziato e grammatico bizantino. Guidò la scuola filosofica di Alessandria dalla morte di Ammonio (523).

Soterico. poeta Soterico (III-IV sec. d.C.), oggetto di recenti studi, è genericamente definito “Oasita” dalle fonti. Si è tentato di specificare tale etnico grazie a dati storico-archeologici; la probabile patria del poeta è l’attuale oasi di Bahariya, dove tra l’altro sorgeva un tempio fondato da Alessandro Magno al termine della pista forse percorsa al ritorno da Siwa. Soterico potrebbe aver commemorato questo fatto in un poema perduto, di cui si ipotizza la sopravvivenza in una parziale parafrasi coliambica.

Dal I Secolo (1d.C -100) … al X Secolo (anno 901-1.000)

Il primo millennio include i secoli dal I sec (1-100) al … V secolo (401 – 500) · VI secolo(501–600 )· VII secolo (601-700) · VIII secolo(701-800) · IX secolo (801 -900) · X secolo(901-1000) …………….· XI secolo (1.001-1.100) …….

Una visione generale fino all’anno 1.000: una ministoria dell’astronomia e della matematica, ministoria che non può essere disgiunta nemmeno dalla filosofia. Ministoria dell’astronomia (vai a).

NOTA. π = 142/45 = 3,1555 . I cinesi Chang Hong e Wang Fau nel III secolo d.C. usarono indipendentemente lo stesso metodo di Archimede, spingendosi fino al poligono di 192 lati e trovarono nel 256 d.C che π = 142/45.

I secolo d.C. (1-100)

ERONE di ALESSANDRIA (?10-70 d.C.), chiamato anche Erone il Vecchio, è stato un matematico, ingegnere e inventore greco antico, che realizzò l’eolipila o «sfera di Eolo» (antenato del motore a getto e della macchina a vapore, di fatto una sfera (metallica), mantenuta in rotazione per effetto del vapore ottenuto al suo interno che fuoriesce con forza da due tubi sottili a forma di “L”.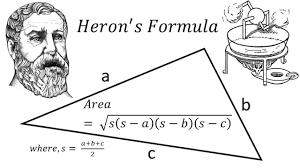) Un tale strumento fu descritto nel I secolo a.C. da Vitruvio nel suo trattato De architectura.Erone produsse molti altri congegni meccanici. La sua collocazione cronologica 10-70, in realtà non è sicura e secondo alcuni storici oscilla fra il I secolo e il III secolo.

Nicomaco di Gerasa (60-120 d.C.), (I-II secolo d.C.) è stato un matematico greco antico di epoca imperiale. Di formazione pitagorica, fu influenzato anche da Aristotele. Le sue opere più note sono l’Introduzione all’aritmetica (Arithmetike Eisagoge) e il Manuale di armonica (Encheiridion Harmonikes). Nell’Introduzione all’aritmetica, Nicomaco si occupa dei numeri, specie del significato dei numeri primi e dei numeri perfetti, convinto che l’aritmetica sia all’origine delle altre discipline matematiche, come la geometria, la musica e l’astronomia. Il teorema di Nicomaco afferma che un quadrato il cui lato è un numero triangolare può essere suddiviso in quadrati e mezzi quadrati la cui somma è un cubo. A Nicomaco si deve il primo riferimento giunto fino a noi del crivello di Eratostene. Boezio realizzò le prime due traduzioni dal greco al latino del trattato introduttivo all’aritmetica e alla musica di Nicomaco di Gerasa. L’Aritmetica boeziana esercitò un notevole influsso sullo sviluppo della matematica medievale. Prima di allora, esistevano i commentari di Apuleio di Madaura, in latino, e di Tâbit ibn Qoran, precedute da quelle greche di Giamblico, Asclepio di Tralle, Filopono e Soterico.

TEONE di SMIRNE (70-135) . Scrisse l’opera Expositio rerum mathematicarum ad legendum Platonem utilium (Esposizione della matematica utile per comprendere Platone) . L’opera è divisa in 2 libri. Il primo libro, contenente la teoria dei numeri: numeri primi, numeri perfetti, numeri abbondanti e simili, mentre una seconda parte tratta della “musica dei numeri” uno studio dell’armonia per mezzo di rapporti, proporzioni e medie -, la musica strumentale (hē en organois mousikē), sugli intervalli e le consonanze, in maniera simile ai lavori di Pitagora e la “musica delle sfere” considerata la più importante e presentata dopo le parti preparatorie precedenti. Nel secondo libro, sull’astronomia, Teone afferma la sfericità della Terra e la sua grande dimensione, descrive occultazioni, transiti, congiunzioni ed eclissi.

MENELAO di Alessandria (70-140). Quasi nulla è noto della vita di Menelao. Pappo (290 circa – 350 circa)e Proclo (412 – 485) lo dicono di Alessandria e Claudio Tolomeo (100-168 d.C.)ricorda due sue osservazioni astronomiche del 98 . Sappiamo che è’ stato un matematico e astronomo greco di cui si conserva un importante trattato di geometria sferica, lo Sphaerica, che è un trattato in tre libri di geometria (e trigonometria) sferica: il più importante sull’argomento conservatosi dall’antichità. Il primo libro introduce il concetto di triangolo sferico e sviluppa la geometria della superficie sferica in analogia a quanto fa Euclide negli Elementi per la geometria piana. Il secondo libro contiene applicazioni all’astronomia. Nel terzo libro si espone la trigonometria sferica ed appare, in particolare, il teorema di Menelao.

Il testo greco dell’opera è perduto, ma se ne è conservata una traduzione araba, che è stata tradotta in latino da Gerardo da Cremona, Francesco Maurolico e Edmond Halley.

{\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=-1.} — **Il teorema di Menelao.**

*Dati un triangolo di vertici* A, B, C , siano dati tre punti D, E ed F che giacciono rispettivamente sulle rette BC, AC , AB. I punti D, E ed F sono allineati se e solo se:

**${\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=-1.$**

In questa equazione, $AF$ , $FB$ , ecc., rappresentano la misura dei segmenti considerati con segno. Per esempio, la frazione $AF/FB$ ha segno positivo solo quando la retta per $D$ , $E$ ed $F$ interseca il lato $AB$ .

**Si tiene anche conto dell’orientamento dei segmenti, cioè: $AB=-BA$**

Autori arabi gli attribuiscono degli Elementi di geometria e un testo di meccanica, ma queste opere non si sono conservate. Alcuni storici moderni gli avevano attribuito anche la composizione di un catalogo stellare, ma su basi che sono apparse inconsistenti a Neugebauer.

IL teorema di Menelao è legato al Teorema di Giovanni Ceva (1647 – 1734) , che ne è il duale.

NICOMACO di Gerasa (0-120 d.C.). Di formazione pitagorica, fu influenzato anche da Aristotele. Le sue opere più note sono l’Introduzione all’aritmetica (Arithmetike Eisagoge) e il Manuale di armonica (Encheiridion Harmonikes). Nell’Introduzione all’aritmetica, Nicomaco si occupa dei numeri, specie del significato dei numeri primi e dei numeri perfetti, convinto che l’aritmetica sia all’origine delle altre discipline matematiche, come la geometria, la musica e l’astronomia.

Il teorema di Nicomaco afferma che “un quadrato il cui lato è un numero triangolare può essere suddiviso in quad”rati e mezzi quadrati la cui somma è un cubo.

A Nicomaco si deve il primo riferimento giunto fino a noi del crivello di Eratostene, il famoso metodo per l’individuazione dei numeri primi, sottolineandone la duplice utilità: decidere se un numero è primo, e stabilire se due numeri sono primi fra loro (confrontandone i fattori primi).

Secondo la tradizione, sarebbe stato espulso dalla scuola pitagorica perché violò il divieto assoluto di diffondere la conoscenza teosofica all’esterno e di conservare una forma esclusivamente orale di tali culti iniziatici di tipo misterico. Boezio realizzò le prime due traduzioni dal greco al latino del trattato introduttivo all’aritmetica e alla musica di Nicomaco di Gerasa. L’Aritmetica boeziana esercitò un notevole influsso sullo sviluppo della matematica medievale. Prima di allora, esistevano i commentari di Apuleio di Madaura, in latino, e di Tâbit ibn Qoran, precedute da quelle greche di Giamblico, Asclepio di Tralle, Filopono e Soterico.

II secolo d.C. (101-200)

APULEIO di Madaura (125-170). Compose numerose opere filosofico-retoriche, in versi e in prosa, in greco e in latino, ma molti dei suoi scritti sono andati perduti, solo alcuni di essi rimasti solo in frammenti. Le metamorfosi, unica opera pervenutoci integralmente, in lingua latina perchè risalente all’epoca romana. L’opera fu nota anche, a Sant’Agostino, col titolo L’asino d’oro. Vedi immagine di Amore e Psiche, episodio delle Metamorfosi. l romanzo è diviso in 11 libri e presenta notevoli somiglianze con un’operetta greca, Lucio o l’asino conservata tra quelle di Luciano di Samosata (il neosofista contemporaneo di Apuleio): le due opere probabilmente sono da ricondurre ad una fonte comune, oltre che al genere della fabula Milesia, cui Apuleio fa spesso riferimento. Lucio, il protagonista, che da uomo diventa asino poi dopo un lungo percorso torna uomo rappresenta la conquista della maturità e dell”equilibrio fra anima e corpo attraverso una serie di esperienze difficili e dolorose. E’ una interessante allegoria della alienazione cui soffre anche l’uomo moderno all’interno della famiglia e della società, che si traduce nell’isolamento del “diverso” e nell’incomunicabilità con i propri simili.

CLAUDIO TOLOMEO (100-170), astronomo, astrologo e geografo greco antico, autore di importanti opere scientifiche, la principale delle quali è il trattato astronomicoCaludio Tolomeo, geografo e astronomo noto come Almagesto. Nell’opera raccolse la conoscenza astronomica del mondo greco basandosi sul lavoro da Ipparco di Nicea (200-120 a.C.). Tolomeo formulò un modello geocentrico, in cui solo il Sole e la Luna, considerati pianeti, avevano il proprio epiciclo, ossia la circonferenza sulla quale si muovevano, centrata direttamente sulla Terra. Questo modello del sistema solare, che da lui prenderà il nome di «sistema tolemaico», rimase di riferimento per tutto il mondo occidentale (ma anche arabo) fino a che non fu sostituito dal modello di sistema solare eliocentrico dell’astronomo polacco Niccolò Copernico (1473-1543), già noto, comunque, nell’antica Grecia al tempo di Aristarco di Samo (310-230 a.C.).L’Almagesto contiene anche un catalogo di stelle, aggiornamento del catalogo di Ipparco di Samo (200-120 a.C.).

π = 377 /120 = 3 (17/20)3 20 = 3,1416666 valore tolemaico (Claudio Tolomeo (100/178? d.C. ),

III secolo d.C. (201-300)

.Pappo di Alessandria, autore di una sintesi della geometria dei secoli precedenti. Plotino l’erede dei filosofi della grecia, Teone di Alessandria (335-405) padre di Ipazia , nell’ambito della geometria .

PAPPO ALESSANDRINO (290-350) Della sua vita si conosce ben poco. L’unica opera pervenutaci è quella intitolata Synagoge, nota anche come Collectiones mathematicae, un compendio di matematica in otto volumi (il primo e parti del secondo sono andate perdute). L’opera copre un ampio ventaglio di argomenti, tra i quali geometria, matematica ricreativa, duplicazione del cubo, poligoni e poliedri. In geometria si hanno altri teoremi attribuiti a Pappo, di cui alcuni sono noti con il nome generico di teorema di Pappo. Tra di essi il Teorema del centroide di Pappo, la Catena di Pappo, il Teorema armonico di Pappo, il Teorema dell’esagono di Pappo, il cosiddetto Teorema di Pappo – Pascal e i Teoremi di Pappo-Guldino.

PLOTINO di Licopoli (203-270). Licopoli è l’antica Asyut egizia., P. è stato un filosofo greco antico. È considerato uno dei più importanti filosofi dell’antichità, erede di Platone e padre del neoplatonismo, a volte identificato in toto col suo pensiero. Le informazioni biografiche su di lui provengono per la maggior parte dalla Vita di Plotino, composta da Porfirio come prefazione alle Enneadi, gli unici scritti di Plotino, che hanno ispirato per secoli teologi, mistici e metafisi-ci pagani, cristiani, ebrei, musulmani e gnostici.

Teone di Alessandria (335-405) padre di Ipazia , nell’ambito della geometria.

IV secolo d.C. (301-400)

Diofanto di Alessandria, il “ padre dell’algebra”, Ipazia, l’unica donna che si sia occupata di matematica nell’antichità.

DIOFANTO Alessandrino (325-409) è stato un matematico greco antico, noto come il padre dell’algebra. La sua Arithmetica fu tradotta nel 1621 in latino da Claude Gaspard Bachet de Méziriac. Della sua vita si sa ben poco. Vissuto ad Alessandria d’Egitto nel periodo tra il III e il IV secolo, alcuni ritengono che sia stato l’ultimo dei grandi matematici ellenistici.Diofanto scrisse un trattato sui numeri poligonali e sulle frazioni, ma la sua opera principale sono gli Arithmetica, trattato in tredici volumi dei quali soltanto sei sono giunti fino a noi^[1]. La sua fama è principalmente legata a due argomenti: le equazioni indeterminate e il simbolismo matematico

IPAZIA di ALESSANDRIA (350/70-415 d.C.)(vai a)

Locandina del film.

Figlia del noto filosofo Teone, studiò fin da giovanissima nella enorme biblioteca d’Alessandria, e ben presto fu a capo della Scuola Alessandrina. Ipàzia è stata una matematica, astronoma e filosofa greca antica. Arrivò a formulare anche ipotesi sul movimento della Terra, ed è molto probabile che cercò di superare la teoria tolemaica secondo la quale la Terra era al centro dell’universo. Ipazia viene ricordata anche come inventrice dell’astrolabio, del planisfero e dell’idroscopio, strumento con il quale si può misurare il diverso peso specifico dei liquidi. Rappresentante della filosofia neo-platonica, fu uccisa, anzi lapidata, per mano di fanatici religiosi, sembra fossero monaci detti parabolani, seguaci di San Cirillo di Alessandria (370 – 444), quindicesimo papa della Chiesa copta, A 1600 anni dalla sua uccisione, nel 415, è considerata una «martire della libertà di pensiero».

TEONE di ALESSANDRIA d’Egitto, (335 circa – 405 ) è stato un filosofo, matematico greco antico. Curò e organizzò l’edizione degli Elementi di Euclide e scrisse commenti alle opere di Euclide e Claudio Tolomeo. Tale edizione fu tradotta in latino da Adelardo di Bath.

V secolo d.C. (401 – 500)

I “grandi commentatori” della matematica greca, Proclo, che commenta Euclide, ed Eutocio di Ascalone, che commenta Apollonio e Archimede.

Severino Boezio (480-524), considerato da molti l’ultimo matematico dell’antichità.

Severino BOEZIO (475/477-524/526 d.C.). Le sue opere ebbero una profonda influenza sulla filosofia cristiana medioevale o Scolastica. Fu seguace della dottrina di Platone tanto che alcuni lo collocarono tra i fondatori, assieme ad Sant’Agostino d’Ippona (354-430), della Scolastica e del pensiero neoplatonico. Da ricordare che Flavio Odoacre (433 (476)493), re degli Eruli, fu riconosciuto, dal semi barbaro Flavio Zenone (425(474)491), Imperatore romano d’Oriente, quale Patrizio d’Occidente, e detto Re d’Italia (in effetti il primo Re). Alla caduta dell’Impero romano d’Occidente nel 476, Odoacre fu ucciso da Teodorico (454(474)526) re degli Ostrogoti che gli successe. Boezio fu il magister officiorum del re Teodorico, il quale esautorò le autorità ecclesiastiche del Papa e dei vescovi, e le sostituì con il suo controllo regale con suoi funzionari civili e militari. Teodorico era ariano, ma tollerò il Cristianesimo. Tuttavia Teodorico, nei suoi ultimi anni, divenne sospettoso di tradimenti e congiure specie da parte dei cattolici. Nel 524 a Pavia, Boezio fu sostituito, quale magister officiorum, da Aurelio Cassiodoro (485-580) e incarcerato e giustiziato, con l’accusa di praticare arti magiche. In carcere compose la sua opera più nota, il De consolatione philosophiae.
Papa Leone XIII (1810(1878)1903) lo riconobbe Santo nel 1883, in quanto le sue vicissitudini avevano molte analogie con la vita di San Paolo, ingiustamente imprigionato e martire. A Boezio (475-526) furono attribuite diverse opere, come la De fide catholica secondo alcuni opera del suo allievo Giovanni, che sembra fosse il futuro Papa Giovanni I (448(523)526). Nell’opera le verità essenziali del Cristianesimo, quali la Trinità, il peccato originale, l’Incarnazione, la Redenzione e la Creazione. Tra le varie opere che gli furono attribuite tradusse in latino le opere di Platone e di Aristotele, e tra le Opere matematiche si ricordano De institutione arithmetica (c. 500) adattamento delle Introductionis Arithmeticae di Nicomaco di Gerasa (c. 160 – c. 220). De Institutione musica (c. 510), si basa su un’opera perduta di Nicomaco di Gerasa e sulla Harmonica di Tolomeo.

Zu CHONGZHI (429–500) giapponese,ottenne buone approssimazio-ni di π, quali: 3,1415926>< π<3, 1415927 e ritrovò la famosa frazione 355/113.

EUCLIDE di Megara (450-380 a.C.). Nato a Megara o a Gela, fondò la scuola megarica. Prima di frequentare ad Atene il suo Maestro Socrate, alla cui morte aveva assistito, aveva studiato la filo-sofia di Parmenide e la sua scuola aveva ospitato Platone costretto a fuggire da Atene per motivi politici. In realtà Euclide di M. tentava una conciliazione tra l’etica socratica e l’ontolo-gia eleatica che egli ben conosceva, come attesta Cicerone che descrive la scuola megarica come la prose-cuzione di quella eleatica collegando Euclide a Senofane, Parmenide e Zenone. Proprio da Zenone Euclide di M., aveva ripreso il metodo dialettico negativo, vale a dire il ragionamento per assurdo diretto alla confutazione non delle premesse ma della conclusione.

Ipparco di Nicea, il “padre della trigonometria” e Teodosio di Bitinia, astronomo. Erone di Alessandria, studioso di meccanica.

$ISIDORO di MILETO (442-537 a.C.). Fu un abile architetto. Grazie al suo lavoro importanti scritti sono stati conservati e trasmessi alle generazioni future. Fu anche un abile matematico, al quale si devono la squadra a T, usata nel disegno tecnico, il metodo di costruzione della parabola con una corda e forse anche ha scritto il libro XV apocrifo degli Elementi di Euclide. (Cfr. Euclide e IPSICLE (190-120 a.C.).$

ARYABHATA (476 d.C., nato a Pataliputra sul Gange). È stato il primo dei grandi matematici-astronomi indiani; la sua opera principale, l’Aryabhatiya, può essere considerata una versione indiana degli Elementi di Euclide. L’opera composta nel 499, è un compendio delle conoscenze matematiche indiane del tempo, composto in versi. E’ divisa in quattro capitoli: il primo tratta di cosmologia, dove fornisce un’approssimazione per la circonferenza della Terra di circa 4967 yojanas, ovvero circa 39968 km (contro 40075 km). Pensava inoltre che il movimento degli astri fosse dovuto ad una rotazione della Terra attorno al suo asse il secondo contiene le regole di misurazione, con le regole per il calcolo di aree e volumi, l’area del triangolo come metà della base per l’altezza, metodi per risolvere equazioni determinate e indeterminate e tratta di progressioni aritmetiche e geometriche; la terza tratta della misura del tempo e dei metodi per determinare la posizione dei pianeti; la quarta parla di trigonometria e del calcolo delle eclissi. Nella parte di Aritmetica presenta una numerazione posizionale, pur senza lo zero. Da un pi greco di 3,1416, sebbene nei calcoli usi spesso il valore di ${\sqrt {10}}\approx 3,1622$ .

PROCLO Licio Diadoco (412 – 485) è stato un filosofo e matematico bizantino, scolarca (a capo) dell’Accademia di Atene. Non fu un matematico creativo ma ebbe il merito di sistematizzare e di portare ai più alti livelli speculativi il neoplatonismo ed è anche noto per i commenti su Euclide, Ipparco, Tolomeo, Erone. ………Il testo “La sfera di Proclo” tradotta da Commandino.

SUN ZI (400-460) o anche Sun Tzu (secondo alcuni vissuto fra il VI e il V secolo a.C.) è stato un leggendario stratega e filosofo cinese. Ha avuto un significativo impatto sulla storia cinese e asiatica, sia come autore dell’Arte della guerra (“Classici” Feltrinelli, 2011), sia come figura mitica e mitizzata.

VI secolo d.C. (501-600)

BRAHMAGUPTA (598-668) famoso matematico e astro- nomo indiano. Gestì l’Osservatorio di Ujjain, e scrisse le opere: nel 628 il Brahmasphuta Siddhānta e ancora nel 665 il Khandakhadyaka. Il Brahmasphuta Siddhānta è la fonte più antica conosciuta (oltre il sistema di numerazione maya), a trattare lo zero come un numero.. Utilizza i numeri negativi e lo zero (quasi in modo moderno). Erroneamente afferma che 0/0 = 0 ma precorre la scrittura 1/0 = Infinito. Trova le soluzioni generali delle equazioni di secondo grado, anche nel caso negativo. In analisi indeterminata, fu il primo a risolvere ax + by = c, dove a, b, c sono numeri interi, con la condizione che il m. c. divisore (a;b) divida c. Scopre che se(a;b)= 1, le soluzioni sono x = p + mb, y = q – ma, (m intero arbitrario). Suggerì anche l’equazione diofantea di secondo grado x² = 1 + py², che prende il nome da John Pell (1611-1685), ma che viene usata per la prima volta nel problema archimedeo dei buoi. Questa equazione attribuita a Pell, venne risolta per alcuni casi speciali da un altro matematico indiano di epoca posteriore, Bhaskara (1114-1185). Va a Brahmagupta il pieno merito di aver fornito tutte le soluzioni intere dell’equazione diofantea lineare, mentre Diofanto di Alessandria si era limitato a dare una soluzione particolare di un’equazione indeterminata. Nel medioevo in India, Brahmagupta utilizza il valore π = radice di 10 = 3,16222776 = molto in uso nel folclore. Sarebbe meglio radice di 9,869 = 3,1414964.

(vai a La formula di Brahamagupta) La formula di Brahmagupta consente di determi-nare l’area di un quadrilatero. Nella sua forma più comune, essa consente di determinare l’area di un quadrilatero inscrivibile in una circonferenza, una volta note le lunghezze dei lati. Ancora interessante il Teorema di Brahmagupta sul triangolo che consente di trovate la lunghezza del segmento di bisettrice di un angolo noto e noti che siano i due lati che lo formano.

OTA. Fu Brahmagupta (598-668) nel V secolo d.C. nel suo Brahmasphuta Siddhānta a trattare lo zero come un numero.. Utilizza i numeri negativi e lo zero (quasi in modo moderno). Erroneamente afferma che 0/0 = 0 ma precorre la scrittura 1/0 = Infinito. Trova le soluzioni generali delle equazioni di secondo grado, anche nel caso negativo. In analisi indeterminata, fu il primo a risolvere ax + by = c, dove a, b, c sono numeri interi, con la condizione che il m. c. divisore (a;b) divida c. Scopre che se(a;b)= 1, le soluzioni sono x = p + mb, y = q – ma, (m intero arbitrario).

VII secolo d.C. (601-700)

BEDA il Venerabile (672-735) Monaco benedettino di origine anglosassone. Ricordiamo il calcolo della Pasqua , la scoperta del meccanismo delle maree. E’ vissuto nel monastero benedettino di San Pietro e San Paolo a Wearmouth (oggi parte di Sunderland), in Inghilterra, e a Jarrow, in Northumberland; è sepolto nella Cattedrale di Durham. È famoso come studioso e autore di numerose opere, tra le quali la più conosciuta è la Historia ecclesiastica gentis Anglorum (Storia ecclesiastica del popolo degli Inglesi), che gli ha valso il titolo di “Padre della storia inglese“. È stato dichiaratosanto e dottore della Chiesa dalla Chiesa cattolica. La memoria liturgica è il 25 maggio nel Rito ambrosiano la memoria liturgica è il 23 maggio. Citato da Dante Alighieri nella Divina Commedia,scrisse su molti altri argomenti, dalla musica alla poesia, ai commentari biblici.

VIII secolo d.C. (701-800)

ALBUMASAR, Jaʿfar ibn Muḥammad, Abū Maʿshar al-Balkhī (787 – 886) è stato un matematico, astronomo, e filosofo persiano, è altresì noto come al-Falaki o Albumasar. Molte sue opere furono tradotte in latino e circolarono ampiamente negli ambienti scientifici europei durante l’età medievale. Scrisse anche una storia dell’antica Persia. verso la fine del XII secolo i libri originali di Albumasar sulla natura cominciarono a essere divulgati in lingua latina, ma rapidamente il suo lavoro fu apprezzato nell’ambiente scientifico del Vecchio Continente, come ben dimostrato dalle “quindici edizioni europee prima del 1500”. Abu Ma’shar sviluppò un modello planetario che qualcuno ha interpretato come un modello eliocentrico. Ciò è dovuto al fatto che le rivoluzioni orbitali dei pianeti sono indicate in modo coerente col sistema eliocentrico piuttosto che come rivoluzioni tipiche del modello geocentrico, e che la sola teoria planetaria conosciuta in cui ciò può aver luogo è la teoria eliocentrica. La sua opera sulla teoria planetaria non è sopravvissuta fino a noi mentre abbiamo i suoi calcoli astronomici, grazie ad Abū Rayhān al-Bīrūnī (vedi in questo elenco).

ALCUINO di York (Albinus Flaccus) (735-804) monaco e grande dotto del tempo. Nel 781 fu chiamato da Carlo Magno(742-814) a dirigere la Schola Palatina” ad Aquisgrana (massima espres-sione culturale dell’epoca) ed istruire sia il Re che i nobili e ad occuparsi della produzione libraria del tempo.

Ricordiamo: Propositiones ad => acuendus juvenes, dove tra gli altri appaiono i classici problemi di traghettamento.

AL KUWARIZMI (780-840)matematico ed astronomo operante a Baghdad presso la corte del Califfo al- Mamun (786-833), fondatore della Beit al Hikma (Casa del sapere). Dal suo nome latinizzato proviene il termine algoritmo con il quale s’indicavano i metodi di calcolo scritto, in contrapposizione ai calcoli effettuati servendosi di gettoni o di tabelle di calcolo. Illustrò il metodo arabo posizionale per scrivere i numeri. Il suo trattato Al-jabr w’almuqabala (il ripristinare e il sovrapporre) ha dato all’occidente il termine Algebra. (vai a scheda e notizie)

Habash al-Hasib Al-MARWAZI (766-869)

HABASH AL HASIB (770-870) . cfr. in questo sito : Matematica/Complementi Scuola Secondaria/Sviluppo storia della Trigonometria.

IX secolo d.C. (801-900)

Abul HASAN Ibn Ishaq (815? – 890), è universalmente noto come l’inventore del Telescopio, ben sette secoli prima di Galileo Galilei (1564 – 1642). Hassan precede al-Biruni (973-1048) e Ibn al Haytham (965 –1039), noto come Alhazen, due altri scienziati musulmani che avevano già aperto la strada al telescopio al mondo. Hasan iniziò a disporre le lenti in modo tale da poter avvicinare gli oggetti celesti. Riuscì a produrre il primo telescopio al mondo nel IX secolo (801-900), che descrive come “un tubo alle cui estremità erano attaccate diottrie“ (le diottrie misurano il potere delle lenti necessario a raggiungere la massima acuità visiva). Fu Abul Hasan a creare le prime bifocali al mondo, che sono occhiali da vista con due poteri ottici. E’ opinione diffusa che gli occhiali siano stati inventati nell’Europa del XIV secolo (1301-1400) e che fu poi Benjamin Franklin (1706 –1790) ad inventare le lenti bifocali. Nel IX secolo gli occhiali da vista erano già stati inventati nel mondo musulmano. Il dispositivo di Abul Hasan fu anche di uso militare, e trovò impiego come binocolo.

NOTA. Fu il pisano Alessandro Della Spina (1240 -1313), un frate domenicano del monastero di Santa Caterina di Pisa, , che avrebbe inventato gli occhiali da vista nel 1280. In quegli stessi anni, i fiorentini attribuirono l’invenzione al loro concittadino Salvino Degli Armati (?? -1317). La critica lo ritiene un personaggio mai esistito, frutto di una falsificazione erudita del XVII secolo, motivata da intenti campanilistici.

ALBATEANO (850-929) Al-ḤARRANI AL-BATTANI membro della comunità Sabea, fu uno dei mas-simi astronomi di tutto il Medioevo islamico e cristiano. Visse a Raqqa (Siria) e dalle sue osservazioni compilò nuove tavole relative al Sole e alla Luna, scoprì il moto dell’apogeo del Sole e attribuì alla precessione annuale il valore corretto di 55 secondi. Calcolò i valori della precessione degli equinozi (54,5″ per anno, o 1° in 66 anni) e l’obliquità dell’eclittica (23° 35′). In Matematica introdusse l’uso dei seni nel calcolo e, in parte, quello delle tangenti e produsse un gran numero di relazioni trigonometriche:

$\tan a={\frac {\sin a}{\cos a}}$

$\sec a={\sqrt {1+\tan ^{2}a}}$

Osservatorio di Al-Battani

Egli risolse anche l’equazione sino = a cosx scoprendo la formula:

$\sin x={\frac {a}{\sqrt {1+a^{2}}}}$

Inoltre, il matematico siriano utilizzò l’idea di tangente di al-Marwāzī al fine di sviluppare equazioni per il calcolo delle tangenti e delle cotangenti, compilando diverse tavole su di esse. cfr. Matematica/Complementi Scuola Secondaria/Sviluppo storia della Trigonometria.

Abu-KAMIL (850-930) – Abū Kāmil Shujāʿ ibn Aslam. La teoria algebrica elaborata da al-Khwarizmi viene completata ed ampliata dall’egiziano Abu-Kamil nel suo Libro sull’al-jabr e l’almuqabala, scritto fra la fine del IX e l’inizio del X secolo. Per questo viene anche chiamato al-Ḥasīb al-Miṣrī, letteralmente “il matema-tico egiziano“. Il suo campo di applicazione fu l’algebra, con riguardo alle equazioni di primo e secondo grado. Ebbe numerosi lettori , fra i quali il pisano Leonardo Fibonacci (1170-1242), uno dei maggiori matematici del medioevo in Occidente, che a lui si isporerà più che ad altri nel compilare il Liber abaci (1202) che porterà in occidente la matematica che si era sviluppata in Oriente. Riporta amche parte dei problemi affrontati da , Abu Kamil, l’egiziano, che utilizzò sistematicamente anche i numeri irrazionali come soluzioni e come coefficienti delle equazioni. Tramite Leonardo Fibonacci, la figura di Abu Kamil l’egiziano fu essenziale per l’introduzione dell’algebra in Europa. quadrato-quadrato-Fra le caratteristiche più salienti della trattazione di Abu Kamil si nota un elevato livello teorico e la tendenza all’aritmetizzazione. Abu Kamil considera ad esempio anche potenze dell’incognita x superiori a 2 e utilizza le locuzioni cubo per indicare x^3.

, Fra le caratteristiche più salienti della trattazione di Abu Kamil si nota un elevato livello teorico e la tendenza all’aritmetizzazione. Abu Kamil considera ad esempio anche potenze dell’incognita x superiori a 2 e utilizza le locuzioni cubo per indicare x³, quadrato-quadrato per x⁴,quadrato-quadrato per x⁴,cosa per x⁵ e così via. LGiovanni SCOTO ERIUGENA (810-877) è stato un monaco irlandese gaelico, cristiano, considerato uno dei più grandi filosofi altomedievali per il contributo nell’ambito speculativo (Periphyseon) e delle opere “La natura dell’Universo” e “Divisione della natura“.

Fu traduttore dell’opera dello Pseudo-Dionigi, che avrà vasta influenza sino alla fine del Medioevo.

THABIT (826 – 901)– Thābit ibn Qurra’ ibn Marwān al-Sābiʿ al-HarrānīAbū lbn-Ḥasan, è stato matematico ed astronomo di religione mandea, noto in Occidente medievale come Thebit o Tebizio. Fu allievo di Muḥammad bin Mūsā,noto come Al-Khwārizmī (vedi in questo elenco), il più anziano dei celebri Banū Mūsā, una famiglia di matematici attiva a Bassora. Thābit studiò matematica, astronomia e filosofia . Famoso per i suoi trattati di mec-canica, astronomia, matematica pura e geometria, Thābit fu pioniere dell’algebra geometrica e propose teorie che portarono allo sviluppo della geometria non-euclidea, della trigonometria sferica, del calcolo integrale e della teoria dei numeri reali. Studiò alcune sezioni coniche (parabola ed ellisse), il calcolo integrale (algoritmi per il calcolo delle superficie e volumi dei solidi) e la statica. Scrisse l’Opuscolo sui numeri amicabili . La copia più antica degli Elementi di Euclide risale al IX secolo, e Thābit ne fece una nuova traduzione pochi decenni più tardi. Tradusse uno studio di Archimede per la costruzione di un ettagono regolare. Lavorò alla teoria dei numeri ed estese il loro uso per descrivere le proporzioni tra elementi geometrici.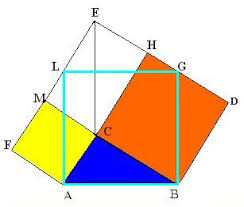 Secondo Copernico Thābit determinò la lunghezza dell’anno sidereo in 365 giorni, 6 ore, 9 minuti e 12 secondi, sbagliando di appena tre secondi.

X secolo d.C. (901-1.000)

ALHAZEN (965 –1039), nome con cui nell’Europa medievale era conosciuto Abū ʿAlī al-Ḥasan ibn al-Ḥasan ibn al-Haytham, è stato un medico, filosofo, matematico, fisico ed astronomo arabo. Fu uno dei più importanti e geniali scienziati del mondo islamico. È considerato l’iniziatore dell’ottica moderna. Restituì alcune opere perdute all’intera umanità: Le coniche di Apollonio di Perga erano in otto libri, dei quali l’ultimo era andato perduto. Ibn al-Haytham fu capace di rielaborare deduttivamente il libro mancante, dandone una stesura del tutto compatibile con la possibile originaria. Ma le traduzioni (fra le quali rilevano gli Elementi di Euclide e l’Almagesto di Tolomeo) lo introdussero anche alla speculazione personale su molte delle materie analizzate, risultando in approfondimenti e riformulazioni che sarebbero rimaste per molti secoli di importanza capitale. La parte più rilevante dei suoi studi è raccolta in 25 saggi di matematica ed in 45 ricerche di fisica (a lui è attribuita la prima, consistente stima dello spessore dell’atmosfera) e metafisica, oltre alla sua autobiografia del 1027. Fu soprattutto nell’ottica che le sue ricerche produssero risultati d’eccezione. Studiando l’ottica euclidea, enunciò teorie sulla prospettiva, della quale focalizzò il suo interesse sui tre punti fondamentali (il punto di vista, la parte visibile dell’oggetto e l’illuminazione), riformulando i modelli geometrici che ne descrivevano le relazioni. Nell’XI secolo (1.001-1.100) Alhazen, pose le basi teoriche per l’invenzione degli occhiali con le sue indagini sulla cornea umana e sugli effetti dei raggi di luce su specchi e lenti. Nel XIII secolo i suoi libri furono tradotti in latino e suscitarono grande interesse per l’ottica e per le sue applicazioni pratiche.

AZOPHI (903-986) – Abd AL-ṢUFI, al-Rahmān, noto come astronomo persiano nel 964. Lavorò come astronomo di corte dell’Emiro Aḍud al-Dawla a Isfahan e per lui realizzò un planisfero celeste in argento che finì più tardi nel Gran Palazzo degli Imam fatimidi Mal Cairo. Descrisse per primo la Galassia di Andromeda, appena visibile ad occhio nudo, descrivendola come una “piccola nube”, pur senza riconoscerne la vera natura, pur essendo la più grande galassia del Gruppo Locale. Ne scrive nel suo Libro delle stelle fisse . Gli è stato dedicato un craterere lunare di 47 km di diametro e l’ asteroide, 12621 Alsufi.

AL-BIRUNI (973-1048) precisamente Abū al-Rayḥān Muḥammad ibn Aḥmad al-Bīrūnī è stato un matematico, filosofo, scienziato e storico persiano, che fornì cospicui contributi nei campi della matematica, della medicina, dell’astronomia. E’ considerato come il “padre dell’indologia”, “padre della geodesia moderna”, il primo antropologo, ed è stato un maestro Sufi. Migliorò l’appros-sima-ione del calcolo del raggio terrestre in 6.339,6 chilometri, migliorando la stima di 6.314,5 km, rispetto alla misura compiuta da Eratostene di Cirene nel 230 a.C. Il cratere Al-Biruni, situato sul Mare Marginis della Luna, è stato così chiamato in suo onore. Gli è stato dedicato un asteroide, 9936 Al-Biruni.

Ibn AL-HAYTHAM (965-1040) noto in Europa come ALHAZEN.Fuuno dei più importanti e geniali scienziati e medico del mondo islamico, operante nell’attuale Irak. Gli era noto, in forma probabilmente pratica il teorema , da noi attribuito a Wilson asserente che:n è primo se e solo se n!+1 è congruo a zero mod n. Fondatore dell’ottica, considerato l’iniziatore dell’ottica moderna. Fu anche chiamato al-Baṣrī (di Bassora), al-Miṣrī (l’egiziano), Avennathan e Avenetan, Ptolemaeus secundus ma, più che altro, fu noto appunto come ALHAZEN corruzione del suo nasab “Ibn al-Ḥasan“. Gli è dedicato l’asteroide, 59239 Alhazen.

AL-HOSEIN (X secolo). A partire dalla relazione pitagorica , dove x, y e z sono i lati di un triangolo rettangolo, egli scoprì lo stretto legame esistente fra la costruzione di triangoli rettangoli con lati interi e la ricerca di numeri congrui. Va rilevato che uno dei più importanti contributi che gli Arabi diedero alla disciplina matematica è, senza dubbio, insito nel tentativo di ricercare la corrispondenza tra geometria ed algebra, evidenziata cinque secoli più tardi da Descartes e Fermat, parallelismo questo che condusse, alcuni secoli dopo, alla nascita della geometria analitica.

AVICENNA (980-1037) Ibn Sīnā, alias Abū ʿAlī al-Ḥusayn, noto come Avicenna, fu riconosciuto autore di importantissime opere nel campo della medicina rimaste incontrastate per più di sei secoli, anzi è considerato come “il padre della medicina moderna” ed indicato come: “il più famoso scienziato dell’Islam e uno dei più famosi di tutte le razze, luoghi e tempi”. Nel settore della fisica, Avicenna fu il primo a impiegare un termometro, per misurare la temperatura dell’aria nei suoi esperimenti scientifici. La cosa era sostenuta da Galileo Galilei, da Cornelius Drebbel, da Robert Fludd e da Santorio Santorio. In meccanica, elaborò una teoria del moto, nella quale poneva una distinzione fra l’inclinazione e la forza di un proiettile, riuscendo a ipotizzare un movimento tendente all’infinito, in presenza di condizioni di vuoto assoluto. È stato considerato un precursore delle leggi di Newton sull’inerzia e sulla forza risultante. Avicenna ipotizzò che la velocità della luce fosse finita e osservò che la percezione della luce è causata dall’emissione di particelle luminose; inoltre provvide a dettagliare una sofisticata spiegazione dell’arcobaleno. Nel 1070, si scrisse che Avicenna avesse risolto alcuni problemi matematico-astronomici nell’ambito del modello planetario. Gli studi astrologici furono scartati in quanto conflittuali con l’Islam.

Gerberto D’AURILLAC (Papa Silvestro II (940-950 (999) 1003), è stato il 139º papa … Fu un prolifico studioso: entrò in contatto e investigò la cultura araba, introdusse in Europa conoscenze di aritmetica e di astronomia, dimostrando una grande versatilità sia nelle scienze applicate, sia in quelle teorico-filosofiche. Si fece conoscere da papi e imperatori per la sua cultura, insegnando e raggiungendo i più alti vertici ecclesiastici a Reims a Ravenna, e poi a Roma quale papa, col nome di Silvestro II. Fu una figura di massima importanza in tutti e tre i suoi campi culturali: il religioso, il politico e lo scientifico. Di sicuro Gerberto è il massimo esponente intellettuale e poliedrico del X secolo e uno dei più importanti di tutto il Medioevo. Gerberto porto l’uso dell’orologio in Occidente, reintrodusse l’uso dell’abaco e operò per la diffusione dei numeri arabi, specie per la sua conoscenza della più avanzata cultura arabo-islamica. Fu inventore di complicati strumenti musicali e astronomici, primo tra tutti l’astrolabio, fece costruire una sirena, funzionante a vapore acqueo, una clessidra ad acqua e sabbia. Progettò e costruì un complesso sistema di sfere, atte a far calcolare le distanze che intercorrevano fra i vari pianeti del sistema solare conosciuto al tempo.

Testa parlante di Papa Gerberto .Il presbitero francese Jacques Paul Migne[1] (1800-1875), ci narra la leggenda di Gerberto, secondo la quale si narra che Papa Silvestro II possedesse una testa di bronzo intelligente in grado di colloquiare con gli astanti. La testa di bronzo rispondeva soprattutto con dei “sì” e dei “no” alle domande che le si rivolgevano sulla politica e sulla situazione della cristianità. Gerberto aveva un automa e forse fu precursore del calcolo binario moderno.

Ali ibn RIDWAN ( 988 – 1061) in seguito ampiamente ricordato come Haly, o Haly Abenrudian, medico e astronomo arabo-egizio. Commentò libri di antica medicina greca, e in particolare opere di Galeno. Il suo Commentario dell’Ars Parva di Galeno fu più tardi tradotta da Gherardo da Cremona (1114– 1187). È anche noto per la sua osservazione della supernova SN 1006 nell’anno 1006, l’oggetto stellare più luminoso della storia, che fu studiata anche da astronomi cinesi nel 1006.. Tale descrizione è all’interno del suo Commentario sull’opera di Claudio Tolomeo nota come Tetrabiblos. Contribuì anche alla teoria dell’induzione. Fu impegnato in una celebre polemica scientifica contro altri medici e scienziati dell’Oriente del tempo.

IBN YUNUS (950-1.009) – Abū al‐Ḥasan ʿAlī ibn Abī Saʿīd ʿAbd al‐Raḥmān ibn Aḥmad ibn Yūnus b. ʿAbd al‐Aʿlā al‐Ṣadafī al-Miṣrī, pseudonimo Ibn Yūnus, è stato un astro-nomo egiziano arabo, di fede islamica, detto il padre dell’Astronomia. Fu un genio della scienza e il primo uomo a misurare il tempo con il pendolo, da lui inventato. Visse durante il regno di Aziz Billah e Hakim bi-Amr-illah, i monarchi fatimidi dell’Egitto. Autore di un colossale Zīj (Tavola astronomica) e un corpus di Tavole di astronomia sferica per il calcolo del tempo liturgico (essenziale per determinare l’inizio del mese lunare di ramadan e la sua fine, o l’inizio del hajj), che seguitarono a essere usate al Cairo fino alla fine del XIX secolo. Il pendolo è stato dunque inventato da Ibn Yunus. L’invenzione del pendolo ha portato alla misurazione del tempo mediante le sue oscillazioni. La sua opera eccezionale è stata riconosciuta come il capolavoro sull’argomento, che ha sostituito l’opera di Tolomeo. Fu tradotto in persiano da Omar Khayyam nel 1079. Gli è stato dedicato un cratere sulla Luna, il Cratere Ibn Yunus.

NOTA. Ignorando l’opera di Ibn Junius, la regolarità nel moto del pendolo fu ristudiata Galileo Galilei (1564–1642) nel XVII secolo (1601-1700). L’invenzione dell’orologio a pendolo è invece attribuita a Christiaan Huygens (1629-1695) che ne depositò il brevetto nel 1656.

SCIENZIATI E FILOSOFI (d.C.) dall’Anno I all’anno 1.000

Habash al-Hasib Al-MARWAZI (766-869)