torna a lista dei Periodi della Matematica.
Matematici e Logici tra 1000 e 1500
Dall’anno 1000 il mondo Islamico fisico-matematico si estese dalle coste dell’Africa del Nord verso tutto il Sud della Spagna e per i successivi tre secoli, la matematica e la filosofia ebbero grande sviluppo, per questo motivo troviamo tra i tanti europei, numerosi e grandi pensatori arabi, cinesi ed indiani.
Leon Battista ALBERTI (1404-1472) (vai a), è stato uno spirito eclettico, fu architetto, scrittore, matematico, umanista, critto-grafo, linguista, filosofo, musicista e archeologo italiano; fu una delle figure artistiche più poliedriche del Rinascimento. Il suo primo nome si trova spesso, soprattutto in testi stranieri. Alberti fa parte della seconda generazione di umanisti di cui fu una figura emblematica per il suo interesse nelle più varie discipline.
ARZACHEL, al-ZARQALI (
1029-1087) ibn Yaḥyā al-Naqqāsh, spagnolo e operò a Toledo e Cordova. Sua opera princi-pale, frutto di innumerevoli osserva-zioni della volta celeste, furono : Le Tavole di Toledo o Tavole toledane, la cui precisione servì da punto di riferimento per la compilazione delle Tavole alfonsine, messe a punto da astronomi 
arabi ed ebrei di al-Andalus durante il regno di Alfonso X di Castiglia. Si occupò di strumenti astronomici e di navigazione, costruì di un planisfero e un astrolabio.Il nome di al-Zarqālī è anche legato a un nuovo e pratico astrolabio piatto facilmente usabile, meno preciso ma molto comodo, di il cui uso infatti, si diffuse dappertutto nei secoli successivi. Gli è stato dedicato il cratere lunare Arzachel, di 97 km di diametro. L‘astrolabio piatto di –> Arzachel.
AVERROE’ (1126-1198) Averroè, nome con cui nell’Europa medievale era conosciuto ʾAbū al-WALID Muḥammad ibn ʾAḥmad ibn Rušd, latinizzato come Aven Roshd e infine come Averrhoës o Averroës è stato un filosofo, medico, matematico, giudice .Nel commentare Aristotele, gli averroisti sostenevano la separatezza dell’intelletto possibile, unico per tutti come quello agente, negando così l’immortalità personale e la provvidenza
Fra. Roger BACON (1214-1294), considerato uno dei maggiori pensatori del suo 
tempo, fu frate francescano italianizzato in Ruggero BACONE. E’ stato un filosofo, scienziato, teologo ed alchimista inglese. Scrisse su: De secretis operibus artis et naturae IV: «Arriveremo a costruire macchine capaci di spingere grandi navi a velocità più forti che un’intera schiera di rematori e bisognose soltanto di un pilota che le diriga. Arriveremo a imprimere ai carri incredibili velocità senza l’aiuto di alcun animale. Arriveremo a costruire macchine alate, capaci di sollevarsi nell’aria come gli uccelli».
Ibn al-BANNA, al-Marrākushī (1256-1321). Matematico ed astronomo. Il cratere Al- Arrakushi sulla Luna porta il suo nome. Figlio di un architetto, studiò a Fès e a Marrakesh, matematica e geometria del suo tempo, traducendo gli Elementi di Euclide in arabo. Fu l’astrologo di corte del sultano meri-nide Abu Sa’id Uthman II. Insegnò a Marrakesh e ad Aghmat. Scrisse tra i 51 e i 74 trattati, su temi diversi quali l’algebra, l’astronomia, la linguistica e la logica. Dal punto di vista astronomico, al-Marrākushī fu fedele agli insegnamenti di al-Zarqālī. La sua opera astronomica principale è intitolata minhāj al‐ṭālib fī taʿdīl al‐kawākib (metodo dello studente per calcolare le posizioni dei pianeti). Come matematico, è noto soprattutto per aver perfezionato un sistema di calcolo che può essere considerato un lontano antenato dei calcolatori manuali, il ḥisāb al-ghubār – e per due delle sue opere: Talkhīs ʿamal al-ḥisāb: un commentario relativo alle tecniche di calcolo, in cui sono trattate frazioni e somme di quadrati e cubi. Rafʿ al-ḥijāb: che si occupa del calcolo delle radici quadrate e la teoria delle frazioni continue. Questo lavoro fu la prima opera dai tempi del matematico e astronomo indiano Brahmagupta a usare una notazione algebrica, che venne poi ulteriormente sviluppata dal suo successore Abu l-Hasan ibn ‘Ali al-Qalasadi due secoli dopo.
Ulugh BEG (1394-1449) fu un sovrano
dell’Impero Timuride, oltre che un impor-tante astronomo e matema-tico. Il nome significa Gran-de (Ulu) Signore (Bek), equivalente al titolo persiano-arabo di Tamer-lano. Il suo vero nome era invece Mīrzā Mohammed Taragai bin Shāhrukh. Fu personaggio di spicco per il suo operato nell’ambito della matematica e delle scienze ‘astronomiche, ovvero trigonometria e geometria sferica, che lo fecero conoscere e stimare anche nell’Occidente cristiano coevo.
BHASKARA (1114-1185), matematico indiano, tratta l’equazione che sarà detta di Pell. Fornisce per π l’approssimazione 3227/1250 che è 3,1416 (1150).
(equazione di Pell (1611-1685). NOTA. La formula risolutiva per una eaquazione di 2° grao è conosciuta come “Formula di Bhaskara” in Brasile.
, 
Hildegard von BINGEN (1098-1179) fu una monaca, mistica, teologa, scienziata, scrittrice, compositrice e musicista tedesca. È considerata una delle figure più importanti dell’Alto Medioevo. I suoi scritti spaziano dalla teologia alla medicina, alla fisica, alla botanica e alla musica.
Al-BIRJANDI (1470?-1528) fu allievo di al-Kashi, dell’Ulugh Beg Observatory, di Samarcanda (Uzbekistan), nato nel 1420 , distrutto nel 1449, ricostruito nel 1908. Operarono nell’Ossevatorio otre al fondatore Ulugh Beg (1394-1449)anche gli astronomi Al-Kashi (1380-1429), e Ali al-Qushji (1403-1474). Nel discutere la struttura del cosmo, al-Birjandi ha proseguito il dibattito di Ali al-Qushji sulla rotazione terrestre . Nella sua analisi di cosa potrebbe accadere se la Terra si muovesse, sviluppa un’ipotesi simile alla nozione di “inerzia circolare” di Galileo Galilei , che descrisse in un test osservazionale.
Jean BORRELL ovvero Johannes BUTEO (1492-1572).
Filippo BRUNELLESCHI (1377-1446) per esteso Filippo di ser Brunellesco Lapi, è stato un architetto, ingegnere, scultore, matematico, orafo e scenografo italiano del Rinascimento. Fu un cultore della prospettiva. Fu l’iniziatore dell’architettura rinascimentale, sia per la realizzazione della grande cupola del Duomo di Firenze sia perché fu il primo a scoprire le regole geometriche del disegno in prospettiva.
Jean BURIDAN (1295/1300- 1361), italianizzato in Giovanni BURIDANO. E’ stato un filosofo e logico francese, maestro delle arti a Parigi e Magnifico Rettore dell’Università di Parigi tra il 1328 e il 1340. La storia dell’asino di Buridano così come la racconta Voltaire: 
«E’ la frivola storiella di un certo asino di cui si discute a scuola? Nella stalla gli vennero portate per il suo pasto due quantità di fieno uguali, della stessa qualità, per molte volte; dai due mucchi l’asino si vide tentato ugualmente, e, drizzando le orecchie, nel mezzo ai due mucchi uguali, concretizzando le leggi dell’equilibrio, morì di fame, per timore di fare una scelta».
Johannes BUTEO(1492-1572) alias Jean BORRELL , matematico ed astronomo. Studiò con l suo maestro Oronzo Fineo (1494-1555). Il suo lavoro prefigurò Guillaume Gosselin (?-?), Jacques Peletier du Mans (1517–1582) e François Viète (1540-1603).
OPERE: Jean Borrel, Opera geometrica, Lugduni, Thomas Bertheau, 1554. De quadratura circuli libri duo, Lugduni, Guillaume Rouille, 1559. – Apologia adversus epistolam Iacobi Peletarii depravatoris Elementorum Euclidis, Lugduni, Michel Jouve, 1562. Vedi il suo maestro Oronzo Fineo (1494-1555).
Giovanni CAMPANO di NOVARA (1220-1296) alias Johannes Campanus, fu matematico ed Astronomo e astrologo. Tra i più importanti scienziati e matematici del secolo XIII (citato da Ruggero Bacone). Nel 1255 pubblicò un’edizione latina degli Elementa geometriae di Euclide con commento all’opera, ie un calcolo degli angoli del pentagono. Il testo, in 
15 libri, fu utilizzato per circa due secoli e sarà stampato a Venezia nel 1482 (Preclarissimus liber elementorum Euclidis). L’opera si basa su una tradu-zione in lingua araba dell’ori-ginale testo greco. Campano ebbe inoltre presente la tra-duzione latina eseguita intorno al 1120 da Adelardo di Bath. Fu cappellano di papa Urbano IV(in un documento della Curia del 1261 pontificia se ne attesta la presenza e se ne parla come di uno dei quattro migliori matematici viventi) e medico personale di papa Bonifacio VIII e viaggiò in Arabia e in Spagna
Chu Shi CHIEH (Cina 1269-1320) , noto per la prima formulazione del triangolo aritmetico (1303) detto poi di Tartaglia o di Pscal che lo riscoprirono. Il triangolo è nel suo libro dal titolo Ssu Yuan Yu Chien.
Nicolas CHUQUET (1445-1488). Scrive Triparty en la science des nombres, copiato in gran parte da Estienne de La Roche (L’arismetique -1520), copiatiura scoperta nell’anno 1870, da un non meglio identificato Aristide Marre, per confronto con il manoscritto di Chuquet, che fu pubblicato da Marre nel 1880. Chuquet inventò una propria notazione per i concetti algebrici e per le potenze, continuando in parte lavoro di Juan de Ortega. Sembra essere stato il primo matematico ad aver utilizzato lo zero e i numeri negativi come esponenti (Oresme introduce i frazionari attorno alla metà del 1300). E’ ricordato come l’inventore della moderna nomenclatura per i grandi numeri, che possono essere chiamati : centinaia, miliaia, milioni, il secondo gruppo bilione, il terzo gruppo trilione, il quarto quadrilione, il quinto quintilione, il sesto sestilione,septilioni, octilioni, nonilioni, deci-lioni…, e così via con gli altri, fino a quando si vuole andare avanti. 112.436.579.839.437.493.183.346.657.829.339.944.677.899 si legge: 112 docilioni,436 undicilioni, 579 decilioni etc.
Nikolaj Kopernik italianizzato in Nicolò COPERNICO (1473-1543).
Nicolò CUSANO (1401-1464). Per quanto interessa l’Astronomia dal 1444 Cusano conobbe Regiomontano, il quale, compreso che Cusano era assertore di una visione eliocentrica dell’Universo, intrattenne con lui un vivo dibattito, essendo egli rimasto un geocentrico, seguace di Claudio Tolomeo. Cusano sosteneva, come dopo di lui Giordano Bruno, proprio contro Tolomeo e Aristotele, che la Terra non è immobile, ma ruota intorno al proprio asse e che non è possibile determinare il centro dell’universo, essendo questo infinito; che le stelle sono simili al Sole, che intorno ad esse possono ruotare dei pianeti e che alcuni pianeti possono essere abitati; produsse quindi delle teorie molto simili a quelle dell’astronomia a noi contemporanea. Si trattava, in effetti, di una visione dell’universo appartenente alla tradizione neoplatonica e che era stata sostenuta anche nel Medioevo, da Ermete Trismegisto (XII secolo). Cusano si occupò inoltre di una possibile riforma del calendario e apportò miglioramenti alle Tavole alfonsine. Oltre a Giordano Bruno (seguace della dottrina cusaniana sulla cosmologia dell’infinito), presero spunto da lui anche Agrippa von Nettesheim, Charles de Bovelles, Erasmo da Rotterdam, Leonardo da Vinci, Niccolò Copernico, Giovanni Keplero, Galileo Galilei, Gottfried Leibniz, Georg Hegel, Carl Friedrich Gauss, Friedrich Schelling e Albert Einstein.
Scipione DAL FERRO (1465-1526). Fu uno degli algebristi del 1500. Insegnò per 30 anni a Bologna. A lui si deve la scoperta della formula risolutiva dell’equazione di terzo grado, anche se in un caso particolare, che tuttavia tenne segreto. Tale formula, dimostrata nelle sua generalità da Tartaglia, è nota come formula di Cardano, che ne fu il divulgatore. Tra i suoi allievi è da ricordare Albrecht Durer (1471-1528). Una raccolta di problemi risolti con l’uso del compasso ad apertura fissa non ci è pervenuto.
Tommaso D’AQUINO (1227-1274) e La Scolastica
Gerberto D’AURILLAC (Papa Silvestro II (940-950 (999) 1003). Fu un prolifico studioso: entrò in contatto e investigò la cultura araba, introdusse in Europa conoscenze di aritmetica e di astronomia, dimostrando una grande versatilità sia nelle scienze applicate, sia in quelle teorico-filosofiche. Si fece conoscere da papi e imperatori per la sua cultura, insegnando e raggiungendo i più alti vertici ecclesiastici a Reims a Ravenna, e poi a Roma quale papa, col nome di Silvestro II.
Piero DELLA FRANCESCA (1413-1492) si occupò di prospettiva. Le sue opere sono mirabilmente sospese tra arte, geometria e complesso sistema di lettura a più livelli, dove confluiscono questioni teologiche e filosofiche. La sua opera fece da cerniera tra la prospettiva geometrica del Brunelleschi e la plasticità di Masaccio, ai suoi quadri una luce altissima schiarisce le ombre e intride i colori.
Albrecht DURER (1471-1528), è stato un pittore, incisore, matematico e trattatista tedesco. Tra gli artisti maggiori del XVI secolo, viene considerato il massimo esponente della pittura tedesca rinascimentale. A Venezia l’artista entrò in contatto con ambienti neoplatonici. Si presume che tali ambienti abbiano sollevato il suo carattere verso l’aggregazione esoterica. Classico esempio è l’opera dal titolo Melencolia I
, realizzata nel 1514, in cui sono presenti evidenti simbologie ermetiche. Dürer conobbe e ammirò l’arte italiana. Nelle sue opere combinò la prospettiva e le proporzioni rinascimen-tali con il gusto tipicamente nordico per il realismo dei dettagli. I volti, i corpi e gli abiti dei suoi personaggi sono raffigurati con minuziosi particolari, gli ambienti sono descritti in maniera realistica e gli spazi sono chiari e ordinati grazie a una precisa griglia prospettica.
Leonardo FIBONACCI (circa 1170- 1240) vedi Leonardo PISANO.
Marsilio FICINO (1433-1499). Nella sua teoria l’anima è «copula mundi» e ha la funzione di connettere Dio alla natura e all’Essere umano, rendendolo così capace di percepire l’amore stesso di Dio e di ascendere in maniera efficace verso la sua contemplazione. Ficino segue il neoplatonismo anche nel sostenere che tutte le cose derivano da Dio e tutte vogliono a Dio ritornare. Espressione di questa tendenza a ritornare a Dio è l’amore, l’amore platonico, che, attraverso la visione della bellezza, eleva l’uomo e rende all’anima le ali per ritornare alla sua patria celeste.
Oronzio FINEO (1494-1555), Oronce Finé, in francese Orontius Finnaeus in latino. E’ stato un matematico, astrologo e cartografo francese. Studiò a Parigi scienze umanistiche e matematiche nel Collège de Navarre. Tra i suoi allievi, il matematico francese Johannes Buteo (1492-1572). Oppostosi al concordato che Francesco I di Valois (1494-1547), Re di Francia, impose alle università nel 1517, subì il carcere fino al 1524, ma fu successivamente nominato dallo stesso sovrano, alla cattedra di matematica del Collège Royal (1532).
ILDEGARDA (vedi BINGEN (von) Hildegard)
Pedro JULIAO – Pietro ISPANO, (1210-1277), fu un filosofo e logico portoghese. Divenne il 187° Papa con il nome di GIOVANNI XXI dal 1976. È l’unico pontefice ad essere apertamente lodato nella Divina Commedia (Paradiso, XII, 135). È probabile che, tra il 1235 ed il 1245, abbia insegnato logica in Spagna e quindi in Francia (forse a Tolosa). Dal 1245 al 1250 un Pietro Ispano risulta essere stato presente a Siena, come medico e docente di medicina, presso lo Studium universitario cittadino, fu definito dai suoi contemporanei «magnus sophista, loycus et disputator atque theologus», per il suo compendio di logica formale Summulae Logicales. In esso Pietro codificò la pratica didattica dei “versi mnemotecnici”. Studia le frasi contenenti vocali-chiave che, estratte, riconducevano a un intero ragionamento quali ad esempio Barbara, Celarent, e similari. La Summulae Logicales fu il manuale di riferimento sulla logica aristotelica in uso nelle università europee per più di 300 anni.
Quin JIUSHAO (1201-1261), cinese fu un matematico e politico ben noto per essere anche un ladro e quindi persona in realtà ben poco affidabile, ma in ogni caso un vero genio matematico. Nel 1257 pub-blica la sua opera dal titolo Shushu Jiuzhang (Trattato di matematica in nove sezioni), dove appare una formula del tutto analoga a quella di Erone ma ricavata in modo indipendente, sebbene il trattato di Qin sia molto più sofisticato. Il capitolo 1 riguarda l’analisi indeterminata; contiene un notevole lavoro sul teorema cinese del resto che si verifica proprio all’inizio del testo. Il capitolo 2 è chiamato Fenomeni celestiali e affronta questioni sul calendario e anche questioni su pioggia o neve. Il capitolo 3 è intitolato Confini dei campi e si occupa di topografia. In questo capitolo viene fornita una formula notevole che esprime l’area di una figura come radice di un’equazione di grado 4. La novità qui è che i coefficienti non sono numeri ma sono funzioni di lunghezze nella figura che sono lasciate non specificate.
Jamshīd Masʿūd al-KASHI (1380-1429) è stato un matematico e astronomo. Iniziò studiando medicina. Dopo aver assistito a un’eclisse di Luna a Kashan nel 1406, scrivsse diverse opere astronomiche. Basandosi sulle Zij-i Ilkhani (tabelle ) di Nasir al-Din al-Tusi, costruì un nuovo catalogo stellare,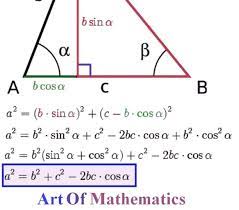 
opera che conteneva anche una collezione di equazioni matematiche utili per l’astronomia come le formule per la trasformazione delle coordinate eclittiche in coordinate equatoriali e tabelle trigonometriche. ale opera è conosciuta come Khāqān zīj (Tavole khaqanidi) e fu dedicata al principe timuride Shah Rukh e al figlio di questi, Uluğ Bek. Il Teorema di Al-Kashi (noto oggi come Teorema di Carnot o del coseno).
Omar KHAYYAM ( ?1048 – 1122, XI Sec d.C.), matematico, fisico ed astronomo. persiano. Scrisse un importante trattato di Algebra che conteneva un approccio geometrico per la soluzione delle equazioni cubiche . Scrisse il poema Rubayat, o Quartine che sono una raccolta di poesie da lui composte nell’XISecolo. .
Estienne de La ROCHE (o de Villefranche) (1470-1530) Scrive L’arismetique nel 1520, in gran parte copiato dal manoscritto di Chuquet (1445-1488).
Raimondo LULLO (1232/4-1315/6) Ramon Llull / Raimundus Lullus. Fu un Filosofo, teologo, mistico e missionario catalano (Palma di Maiorca) detto doctor illuminatus
Peregrino Pietro di MARICOURT (XIII secolo). A lui si deve il merito di aver individuato per primo i poli magnetici inseparabili, che chiamò POLO NORD e POLO SUD. La sua opera fondamentale, stampata per la prima volta nel 1558, è l’Epistola de magnete, indirizzata a tale Sigero di Foucaucourt. Maricourt rigettò la teoria della repulsione tra poli omonimi, mentre enunciò correttamente la magnetizzazione per contatto. Contiene la procedura per la costruzione di una rudimentale BUSSOLA. Maricourt non era tuttavia conscio della declinazione magnetica, il che costituisce una delle maggiori falle della sua teoria.
MADHAVAN di Sangamagrama (1350 – 1425) matematico e astronomo indiano uno dei più grandi del Medioevo, per essere stato il primo a far uso degli sviluppi in serie. Fu il fondatore della Scuola matematica del Kerala ed è considerato da vari studiosi il padre fondatore dell’analisi matematica perché compì il passo decisivo che permise di passare dalle procedure finite dei matematici antichi a quelle infinite attraverso il concetto di passaggio al limite, nucleo della moderna analisi classica. Ha calcolato il valore di π con 11 cifre decimali, il valore più esatto di π dopo quasi mille anni. ed ottenne un’approssimazione per π di 11 cifre che equivale alla frazione : 2 827 433 388 233 / 900 000 000 000 = 3,14159265359. Trovò la formula :
Francesco MAUROLICO (1494-1575). Nel 1534 Francesco Marulì cambiò il proprio cognome in Mauro lyco (dal significato di “lupo occulto”), facendo parte di un’accademia messinese. Nel 1521 ottiene l’ordinazione sacerdotale e, conseguentemente, qualche beneficio ecclesiastico, fu nominato nel 1550 abate del monastero di Santa Maria del Parto a Castelbuono da Simone Ventimiglia marchese di Geraci, del Maurolico allievo e mecenate. Intuì e sviluppò il principio di induzione matematica, studiò metodi per la misurazione della Terra, fece osservazioni astronomiche (come quella della supernova apparsa nella costellazione di Cassiopea), fornì le carte geografiche alla flotta cristiana in partenza dal porto di Messina per la Battaglia (navale) di Lepanto, del 7 ottobre 1571, nel corso della guerra di Cipro, tra le flotte turco-musulmane dell’impero ottomano che subirono una grande disfatta contro quelle cristiane della Lega Santa. I turchi misero in salvo appena trenta galee e persero circa 35.000 uomini tra morti, feriti e prigionieri.
Guglielmo di MOERBEKE (1215–1286), curò la prima traduzione in latino dei frammenti superstiti di Diocle (II-II Sec. a.C.). Gerald James Toomer (1934), nel 1976, pubblicò il testo arabo. Domenicano (1215 circa – 1286), arcivescovo di Corinto dal 1278. Molto importante la sua vasta attività di traduttore di opere greche, specialmente di Aristotele e dei suoi commentatori, e di revisore di traduzioni già esistenti, svolta anche per incarico di Tommaso d’Aquino cui era legato da fraterna amicizia. Di Aristotele egli tradusse le Categoriae, il Peri hermeneias, il III e il IV libro del De coelo, i Meteorologica, i Parva naturalia, l’XI libro della Metaphysica (mancante nella traduzione fino allora in circolazione), la Poetica, la Politica, la Rhetorica, i Libri de animalibus, e rivide le versioni della Physica e del De anima di Giacomo Veneto, dei primi due libri del De coelo e dell’Ethica Nicomachea di Roberto Grossatesta, della Metaphysica (la cosiddetta “translatio media”). Particolare importanza ebbero anche, per lo sviluppo del pensiero e della scienza medievali, le sue traduzioni di alcune opere di Proclo (Elementatio theologica, De fato, De providentia, De malo, queste ultime tre perdute nel testo greco, il commento al Parmenide di Platone) e di numerosi scritti di matematica e di medicina.
NASIR Eddin vedi al-TUSI (1201-1274),
Giordano NEMORARIO (1225 – 1260), è stato un matematico e astronomo italiano. Autore del trattato di algebra Algorithmus demonstratus ed interessante è il Liber Iordani de ponderibus (tre opere distinte). Una parte , che lo chiama il “precursore di Leonardo da Vinci”, segna notevoli progressi sulla statica greca: in essa è introdotta la nozione di componente del peso secondo una data direzione e vi è tacitamente applicato, per stabilire l’equilibrio della leva, il principio: la forza che può elevare un peso a una certa altezza può elevare un peso m volte più grande a un’altezza m volte più piccola; principio che verrà assunto più tardi da Cartesio a fondamento della sua statica che si trasformerà poi nel principio dei lavori virtuali.
William di OCCAM (1295-1347) oppure Ockham, italianizzato in Guglielmo D’OCCAM , è stato un frate francescano teologo, filoso-fo, logico inglese. Il principio lo-gico del Rasoio di Occam (nova-cula Occami), detto anche “prin-cipio di economia” ritenuto alla base del pensiero scientifico moderno. Si tratta di un principio metodologico che, tra più ipotesi per la risoluzione di un problema, indica di scegliere, a parità di risultati, quella più semplice, ovvero la più breve senza ridondanza di parole. Usa il motto : «è inutile fare con più mezzi (parole) ciò che si può fare con meno (parole)» .
Nicola ORESME, vescovo di Lisieux (1323-1382). Costruì un sistema a reticolato che precorre le coordinate cartesiane, ai fini di studiare matematicamrnte i fenomeni naturali. Introduce gli esponenti frazionari (gli esponenti negativi saranno introdotti da Chuquet nel 1494).
Juan de ORTEGA (1480-1568) matema-tico spagnolo dell’ordine dei Domenica-ni. Insegnò matematica commerciale in Aragona e Italia. In una sua opera pubblicata nel 1512 a Barcellona, Tractado subtilisimo d’arithmetica y de geometria, offrì un metodo sofisticato di estrazione delle radici, che prefigurava le equazioni di Pell-Fermat. Il trattato fu ripubblicato a Roma nel 1515, Messina nel 1522 e Siviglia nel 1552. Come alcuni matematici, a lui successivi, quali Marino Ghetaldi (1568-1626), Adriano Romano (1561-1615), Renè Descartes (1596-1650), fu fra i pochi a usare il “+” come simbolo di addizione. Il suo metodo fu continuato da Nicolas Chuquet (1445-1488).
Luca PACIOLO (1445-1517), matematico ed economista
Leonardo PISANO detto IL FIBONACCI (1170-1240) (vai a) fu un grande matematico, e un viaggiatore che, grazie ai suoi contatti con il mondo arabo, introdusse elementi culturali di enorme importanza, che hanno cambiato l’intera cultura del mondo occidentale.
Willem van MOERBEKE (1215 – 1286 circa), fiam-mingo è stato un domenicani, arcivescovo cattolico e traduttore di numerosi scritti di matematica e di medicina. Fu traduttore di opere greche, di Aristotele e fu revisore di traduzioni già esistenti, anche per incarico di Tommaso d’Aquino cui era legato da fraterna amicizia. Di Aristotele egli tradusse le Categoriae, il Peri hermeneias, il III e il IV libro del De coelo, i Meteorologica, i Parva naturalia, l’XI libro della Metaphysica la Poetica, la Politica, la Rhetorica, i Libri de animalibus, e rivide le versioni della Physica e del De anima di Giacomo Veneto, dei primi due libri del De coelo e dell’Ethica Nicomachea di Roberto Grossatesta, della Metaphysica (la cosiddetta “translatio media”).
Giordano NEMORARIO (1225 – 1260) alias Jordanus Nemorarius/ Jordanus de Nemore/Giordano di Nemi/ Gior-dano di Sassonia di incerta nazio-nalità, è stato un matematico e astro-nomo italiano.
Ali al-QUSHJI (1403-1474), nome turco di Alāʾ al-Dīn ʿAli ibn Muhammed, è stato un astronomo, matema-tico e fisico turco o persiano, ed anche un importante scienziato centro-asiatico, che si trasferì nell’Impero ottomano qualche tempo prima del 1472.
DUNS SCOTO John (1265-1303), scozzese e frate francescano, cono-sciuto anche con l’epiteto di Doctor Subtilis, [da non confondere con l’irlandese Giovanni Scoto Eriugena, in lat.: Johannes Scotus Eriugena (810 ->877), lista entro il mille]. E’ stato un filosofo e teologo di grande profondità . È stato beatificato da papa Giovanni Paolo II il 20 marzo 1993. Papa Giovanni Paolo II nella catechesi del 5 giugno 1996 definisce Scoto «Dottore dell’Immacolata» perché con la sua dottrina ha offerto alla Chiesa la chiave per superare le obiezioni circa l’Immacolata Concezione di Maria. Per questo suo apporto alla dottrina cattolica, già papa Paolo VI lo aveva chiamato il «Dottore Sottile e Mariano». Il teorema asserente che “ex falso sequitur quodlibet” (ossia: “dal falso segue qualsiasi cosa”), è attribuito, per tradizione, a Duns Scoto, sebbene in realtà sia opera di un autore sconosciuto, e la cui conoscenza, peraltro, risale all’antichità poichè era già noto, ad esempio, alla scuola megarica. Ci si riferisce ad esso come Teorema dello pseudo-Scoto.
REGIOMONTANO (Johannes MULLER) – (1436-1476) è stato un matematico, astronomo e astrologo tedesco. Ebbe fama di matematico e astronomo prodigio fin dalla prima giovinezza; a soli undici anni divenne uno studente all’Università a Lipsia, in Sassonia. Tre anni dopo continuò gli studi in Austria, all’Alma Mater Rudolfina, l’Università di Vienna. Là divenne pupillo ed amico di Georg von Peurbach. Nel 1457 ottenne il titolo di “Magister artium” e tenne lezioni di ottica e letteratura antica. Costruì astrolabi per Mattia Corvino, re di Ungheria e per il cardinale Giovanni Bessarione; nel 1465 costruì una meridiana portatile per Papa Paolo II. La sua collaborazione con Peurbach lo portò agli scritti di Nicola Cusano, che sostenevano la visione eliocentrica dell’Universo. Regiomontano rimase tuttavia un geocentrico, un seguace di Tolomeo.
Gregoire de SAINT-VINCENT (1584-1667) , gesuita e matematico di origine fiamminga, noto soprattutto per i suoi studi sulla quadratura del cerchio.
Michael STIFEL (1487-1567) . Monaco agostiniano, sostenitore di Martin Lutero e docente all’università di Jena. Scrive nel 1544, il trattato Arithmetica integra, con la formula di Stifel,xx sulla somma dei coefficienti nel triangolo di Tartaglia (1499-1557). Ritenuto in Germania l’ideatore stesso del sopraccitato triangolo, è noto anche per essere stato uno dei precursori dei logaritmi ed aver osservato tra i primi le proprietà delle potenze. esiste uno Stifel del 1909.
Nicolò TARTAGLIA da Brescia (1499 -1557)
Nasir Eddin al-TUSI (1201-1274), matematico e filosofo persiano. Fu uno dei primi a tradurre in arabo le opere Euclide, Apollonio e Tolomeo e diede contributi originali sia alla matematica che alla astronomia.
Paolo UCCELLO (1397-1475)
Johann WERNER (1468 – 1522) è stato un eminente cartografo, mate-matico e religioso tedesco. In campo matematico, lasciò un contributo in trigonometria con le formule di prostaferesi e le formule di Werner. Queste ultime svolgono un ruolo chiave nell’algoritmo di prostaferesi, un metodo per semplificare il calcolo manuale delle moltiplicazioni.
Erazmus Ciolek WITELO, detto VITELLIONE (1230-1275). Nativo della Slesia, è stato un monaco cristiano, matematico, fisico, filosofo e teologo polacco.
al-ZARQALI (1029-1087) vedi ARZACHEL.