Matematici dal 1700 al 1800

torna a lista dei periodi della M.

Matematici dal 1700 al 1800

NOTA. Il calcolo di π nel 1700  (vai a). Trattiamo coloro che calolarono le cifre da 19 (1713) a 152 (1718).

NOTA. MATEMATICI NAPOLETANI DEL 1700 (vai a) Trattiamo: Colecchi -De Filippis – Flauti – Giordano – Lauberg che in ogni caso sono da approfondire.

 

Pietro ABBATI-MARESCOTTI (1768-1842) Gli Abbati Marescotti sono una casata modenese iscritti al ceto Conservatorio fin dal sec. XVI la quale ha dato i famosi pittori Niccolò (??? – 1571) ed Ercole (??? – 1613), da un Pietro di Paolo proveniente da Castelnuovo di Sotto nel Reggiano, aromatario ducale, morto il 30 gennaio 1702. Un suo nipote Pietro di Bernardino (1693-1762) fu valente matematico e studioso di idraulica ed anche buon letterato.

Pier Paolo Abbati-Marescotti (1936-  ) – Modena – Meccanica Razionale.

Maria Gaetana AGNESI (1718-1799)(vai a)  LaVersiera di A.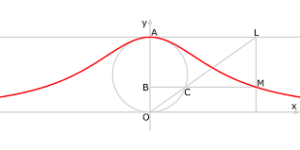

Maria Gaetana Agnesi è stata una matematica, filosofa, teologa, accademica e filantropa italiana. Riconosciuta come una delle più grandi matematiche di tutti i tempi, fu la prima donna autrice di un libro di matematica e la prima a ottenere una cattedra universitaria di matematica presso l’Università di Bologna. La Agnesi ha contribuito in modo significativo allo sviluppo dell’analisi matematica e dell’algebra. Vedasi Articolo (2019) : Maria Gaetana Agnesi, matematica geniale suo malgrado, Redazione Youmanist. Vedasi anche: Eugeni Franco (2021). L’emancipazione della donna e il suo tardivo accesso al mondo della scienza, in questo sito e in corso di stampa su Bollettino dell’Afsu.

Maria Gaetana AGNESI (1718-1799) è stata una matematica, fisica e filosofa italiana. È stata la prima donna a ricoprire la cattedra di matematica all’Università di Bologna. 

•  

Jean-Robert ARGAND (1768-1822). Nel 1806, pubblicò a proprie spese un libro in cui veniva esposta l’idea dell’interpretazione geometrica dei numeri complessi, struttura che da lui e da Gauss fu detto piano di Argand-Gauss (Piano complesso), trasformando  un numero complesso in un vettore. Diede  una dimostrazione (non del tutto corretta) del Teorema fondamentale dell’algebra. ; Argand sembra essere stato il primo a trattare equazioni algebriche a coefficienti complessi.

Giovanni Barsotti (1799 – 1870) è stato un matematico italiano. E’ stato un insegnante di meccanica razionale all’Università di Lucca e poi in quella di Pisa. Membro dell’Accademia lucchese. Il 19 novembre 1843 divenne socio dell’Accademia delle Scienze di Torino. Viene ricordato per alcune ricerche sulle equazioni algebriche e le funzioni iperboliche.

Laura BASSI (1711-1778) fu la prima donna in Italia a laurearsi in fisica (filosofia e matematica), è stata una accademica italiana. Nel 1739 fu nominata professoressa di fisica sperimentale presso l’Università di Bologna, divenendo la prima donna al mondo a ottenere una cattedra universitaria. La Bassi prestò servizio come professoressa per oltre 40 anni e fu una delle scienziate più importanti del suo tempo. Le sue ricerche si concentrarono sulla meccanica, l’elettromagnetismo e l’ottica. Bassi fu anche una scrittrice prolifica e pubblicò diversi libri e articoli scientifici. Morì a Bologna nel 1778. La vita e le opere di Laura Bassi hanno ispirato molte altre donne a seguire le sue orme e a intraprendere carriere scientifiche. La Bassi è un’importante figura nella storia della scienza e del femminismo.

BERNOULLI famiglia  (vai all’albero genealogico)

Friederich Wilhelm BESSEL (1748-1846)

Etienne BEZOUT (1730-1783) si occupò di matematica studiando Euler. Insegnò nelle scuole militari, e fu esaminatore per l’ammissione in Marina. Scrisse Cours de mathématiques à l’usage des Gardes du Pavillon et de la Marine, 4 vol. (1764-69) che    fu molto popolare, e tradotto in diverse lingue: fu usato all’Università Harvard. Nel 1769 Bezout  fu associato all’Accademia delle scienze francese.  L’identità di Bachet-Bézout, afferma che se a e b  sono interi (non entrambi nulli) e il loro massimo comune divisore è d, allora esistono due interi x ed y tali che ax+by = d. Sussiste anche il seguente: Teorema di Bezout : Due curve algebriche di ordini m ed n, prive di componenti comuni si incontano in mn punti, considerando i punti reali e complessi ciascuno con la sua molteplicità. 

Jacques Philippe BINET (1786-1856)

Farkas Wolfang BOLYAI – padre (1775-1856). A 12 anni l fu nominato tutore del figlio  del conte Kemény,  una delle famiglie principali della nazione.  Nel 1796 e iniziò a studiare matematica sistematicamente nelle università tedesche, prima a Jena e quindi a Gottinga. Nel 1799 sposò Zsuzsanna Benkő e, nel 1802, nacque il loro figlio, János Bolyai, che più tardi sarebbe diventato un matematico ancora più famoso del padre. Accettò un posto di insegnante di matematica e scienze al collegio calvinista di Marosvásárhely (Târgu Mureș in rumeno), dove trascorse il resto dei suoi giorni. Vedi Janos BOLYAI (figlio) (1802-1860).

Bernard BOLZANO (1781-1848). origine italiana ma nato e morto a Praga, dove fu professore di Filosofia delle Religioni.Cultore di logica, matematica e sociologia. I suoi scritti di Analisi Matematica rimasero inediti, nonostante l’elevato rigore e il profondo contenuto, anche rispetto ai contemporanei. Teorema di Bolzano–Weierstrass : “Un insieme infinito e limitato ammette almeno un punto di accumu-lazione.”

 

Antonio Maria BORDONI (1788-1860). Fu allievo di Brunacci.  Subito dopo la laurea a Pavia nel 1807, fu incaricato dell’insegna-mento della matematica e della fisica alla Scuola Militare, istituita da Napoleone a Pavia, presso il Collegio Ghislieri. A Pavia nel 1816-17 fu supplente del Brunacci alla cattedra di Calcolo sublime, geodesia e idrometria; nel 1817-18 fu professore di Matematica pura ed elementare, tornando, dopo la morte di Brunacci (1818), a insegnare Calcolo sublime,  Idrometria e geodesia. Mantenne l’insegnamento del calcolo sublime fino al 1841, quando «una malaugurata riforma degli studi diede al governo austriaco l’occasione, forse desiderata, di restringere il campo d’azione del Bordoni», conservò invece quello della Idrometria e geodesia fino al 1852. Dal 1844 alla morte fu inoltre Direttore degli studii matematici. Fra i suoi più noti allievi vi furono Francesco BRIOSCI (1824-1897) , di cui Bordoni fu relatore di tesi nel 1845, Luigi Cremona, Eugenio Beltrami, Felice Casorati e Delfino Codazzi. È stato intitolato a suo nome l’Istituto Statale d’Istruzione Superiore “A. Bordoni” a Pavia.

(Gabrielle) Emile du BRETEUL, marchesa di CHATELET (1706-1749) è stata una matematica, fisica e letterata francese. È considerata uno dei più grandi ingegni del XVIII secolo. È stata una delle prime persone a tradurre in francese le opere di Isaac Newton. Figura colta e spregiudicata in antitesi con la Agnesi colta e in odore di santità.  (per saperne di più). Vedasi : Eugeni Franco (2021). L’emancipazione della donna e il suo tardivo accesso al mondo della scienza, in questo sito e in corso di stampa su Bollettino dell’Afsu.

 

Charles Julien BRIANCHON (1783-1864)                      Teorema di Brianchon.

Vincenzo BRUNACCI (1768-1818). Studiò nell’Università di Pisa, medicina, astronomia e matematica con Pietro Paoli (1759-1839), laureandosi in Medicina nel 1788 e nominato professore di Fisica. Fu anche  Ispettore generale della Pubblica Istruzione del Regno Italico (di Napoleone). Nel 1799 andò in Francia e al rientro occupò la cattedra  di Paoli a Pisa. Nel 1801 si trasferì a Pavia come rettore. Nel 1803 fu membro dell’Istituto Nazionale Italiano,  e nel 1806 della “Società italiana delle Scienze” . Furono suoi allievi Antonio Bordoni, Giovanni Taddeo Farini e Ottaviano Fabrizio Mossotti (maestro di Enrico Betti). 

Sebastiano CANTERZANI (1734-1818)  è stato un matematico e fisico bolognese, figlio del matematico Giuseppe Canterzani, frequentò le scuole secondarie dai Gesuiti. Nel 1760 fu nominato professore di matematica all’Università di Bologna. Nel 1766, allorché Francesco Maria Zanotti divenne presidente dell’Istituto delle scienze di Bologna, Canterzani ne fu nominato Segretario. I suoi numerosi studi riguardarono soprattutto l’analisi matematica. Si interessò anche di astronomia e partecipò al gruppo di studio che il 6 giugno 1761 calcolò l’orbita di Venere. Fu allontanato dall’insegnamento nel 1796 con l’arrivo a Bologna delle truppe francesi, ma riebbe la cattedra nel 1802.

Lazare Nicolas CARNOT (1753-1823)

Augustin  CAUCHY (1789-1857), matematico ed ingegnere francese. Insegnò all’Ecole Polytecnique e all’Ecole des Pons e Chausses, fondate da Gaspard Monge e dopo il 1816 insegnò alla Sorbona e al College de France e fu socio dell’Accademia delle Scienze al posto di Monge,che non giurò per il Re Luigi XVIII della restaurazione post napoleonica. Ma lo stesso Cauchy non giurò per la Repubblica del 1830 e andò in esilio. Nel 1852 fu dispensato dal giuramento da Napoleone III e riprese l’insegnamento. Ha avviato il progetto della formulazione e dimostrazione rigorosa dei teoremi dell’analisi infinitesimale basato sull’utilizzo delle nozioni di limite, perfezionando l’idea originale di D’Alambert (1717-1783),  e di continuità nel suo libro Cours d’Analyse del 1821. Ha dato anche importanti contributi nei suoi 789 lavori, tra cui le successioni di Cauchy, il problema di C. per le eq, differenz. ordinarie, il teorema di Cauchy-Kolevska per le eq. differ. alle derivate parziali, la teoria delle funzioni di variabile complessa, nella fisica matematica si occupò della Teoria dell’elasticità e della dispersione della luce. La sistematicità, il rigore  e il livello dei suoi lavori lo collocano tra i padri dell’analisi matematica.

Tiberio CAVALLO (1749-1809) fisico, va a Londra nel 1777. Amico di Alessandro Volta (1745-1827). Scrisse 3 volumi sull’elettricità in inglese.

Michel CHASLES (1793-1880). Dopo brillanti studi Chasles entra all’École Polytechnique nel 1812 sotto la guida di Siméon Denis Poisson. Diventa professore nel 1841. Nel 1846 viene istituita per lui una cattedra di geometria superiore alla Sorbona. Nel 1851 viene eletto membro dell’Accademia delle scienze francese. Ddiventa membro della Royal Society il 15 giugno 1854. I suoi lavori di geometria gli varranno la Medaglia Copley nel 1865. In geometria proiettiva   parallelamente ai lavori di August Ferdinand Möbius, Julius Plücker e Karl von Staudt in Germania, egli completò attraverso un approccio sintetico la geometria proiettiva che Jean Victor Poncelet e Joseph Diaz Gergonne avevano già rinnovato partendo dai lavori di Girard Desargues. Si occupò delle omografie, introdusse il concetto di birapporto di 4 punti allineati e a lui si deve il termine omotetia. Sulle coniche dimostrò il seguente risultato: “Siano date cinque coniche (ellissi, parabole o iperboli) in un piano; esistono 3264 coniche tangenti a quelle cinque” (queste coniche possono essere reali o complesse). Formulò inoltre diversi importanti teoremi tutti chiamati Teorema di Chasles tra i quali il seguente: “Se fissiamo i punti A, B, C, D, su una conica γ e consideriamo un generico punto P di γ , allora il birapporto delle rette PA, PB, PC, PD, non varia al variare di P su γ. Viceversa dati quattro punti A, B, C, D ed un numero reale k il luogo dei punti del piano per cui il birapporto delle rette PA, PB, PC, PD, sia uguale a k è una conica passante per A, B, C, D”. Parte della sua opera è pubblicata nel suo “Traité de géométrie supérieure” (1852) (Trattato di geometria superiore).

Alexis CLAIRAUT (1713-1765) opere didattiche

 

 

 

Ottavio COLECCHI (1773-1847),di Pescocostanzo, frate domenicano,   è stato un filosofo e matematico napoletano. Avviato al sacerdozio fu domenicano con il nome di fra Tommaso. Le prime due opere matematiche furono Memoria sulle forze vive e, la seconda, Riflessioni sopra alcuni opuscoli che trattano delle funzioni fratte. Nel 1811 Colecchi fu eletto socio della Accademia Pontaniana presentando la memoria, rimasta inedita, Sul minimo dell’azione. Nel 1812 divenne professore di calcolo sublime al Reale Collegio della Nunziatella. Fu sospettato sia di essere liberale che ateo. Dopo la caduta di Murat, fu in Russia dal 1817 al 1818, precettore dei figli dello zar. La conoscenza diretta che egli ebbe delle opere kantiane, che diffuse sia con l’insegnamento privato sia con le proprie memorie (edite in 3 voll. nel 1843 col titolo Quistioni filosofiche), ebbe grande importanza per la formazione del pensiero speculativo napoletano. Nel 1819 il C. era di nuovo a Pescocostanzo ed il 10 novembre di quell’anno ottenne con un regio decreto la cattedra di fisica e matematica sublime al liceo dell’Aquila e con decreto del 15 maggio 1820 fu nominato socio corrispondente della Reale Società economica.  Tornato in Italia, aprì a Napoli una scuola di filosofia. 

Nicolas de CONDORCET (1743-1794) – 51, ovvero Marie-Jean-Antoine-Nicolas de Caritat, marchese di Condorcet, è stato un matematico, economista, filosofo e politico rivoluzionario francese. Fece parte del gruppo degli “enciclopedisti”, con una proficua collaborazione con gli stessi fondatori D’Alembert (1717-1783) e Diderot (1713-1784), ma anche collaborando con il filosofo Paul Henri d’Holbach (1723-1789) e del grande uomo dell’Illuminismo François-Marie Arouet (1694-1778) detto Voltaire, che massone di fatto, fu  iniziato nella loggia francese Le Nove Sorelle il 7 aprile 1778 (pochi mesi prima della sua morte). Condorcet a sua volta era membro della  Loggia parigina Le nove sorelle, del Grande Oriente di Francia, a suo tempo diretta anche da Bejamin Franklin, ambasciatore in Francia delle nascenti colonie americane. Come matematico scrisse nel 1765 Sul calcolo integrale e nel 1768 Saggi di analisi e nel 1785 Saggio sull’applicazione dell’analisi alla probabilità delle decisioni prese a maggioranza di voti, dove tentava di applicare forme di calcolo matematico ai fenomeni sociali. Nel 1769 entrò a far parte dell’Académie des Sciences, di cui divenne segretario nel 1773. Nel 1782 fu eletto all’Académie Française. Per l’ Enciclopedie vedi NOTA dopo Diderot. 

 

Gabriel CRAMER (1704-1752)  (vai a)

 

 

 

Jean-Battiste le Rond detto D’ALAMBERT (1717-1783)- 66, matematico, fisico, astronomo, filosofo e enciclo-pedista francese, tra i più importanti protagonisti dell’Illuminismo. È famoso per la formulazione di un principio sull’equilibrio meccanico che porta il suo nome.  E’ lui che per primo introduce il concetto di limite, che in ogni caso fu ripreso e reso più rigoroso nell’opera di Augustin -Cauchy (1789-1857). Interessante un notevole teorema, oggi noto come “teorema di d’Alembert”, in cui prova l’esistenza di n radici per qualsiasi equazione algebrica di grado n nel campo dei numeri complessi. Nel 1744, introduce le derivate parziali. Tra il 1739 e il 1741 pubblicò due opere fondamentali “Memorie sul calcolo integrale” e “Memorie sulla rifrazione dei corpi solidi” . Nel 1743 venne stampato il suo “Trattato di dinamica”, dove è sviluppato il principio che porta il suo nome. Seguirono il “Trattato sull’equilibrio e sul movimento dei fluidi” e il “Trattato sulle cause generali dei venti”, dedicato a Federico II, re di Prussia, anche lui massone. Nel 1749, a seguito degli importanti risultati conseguiti nell’ambito delle equazioni differenziali alle derivate parziali, fu chiamato a dirigere l’Encyclopédie (detta di Diderot e D’Alambert)  con Denis Diderot (1713-1784) e con Condorcet (1713-1784), ma dopo la censura (dopo la condanna nel lavoro L’esprit di Claude-Adrien Helvétius (1715-1771), ex collaboratore) si ritirerà, e sarà Diderot da solo a continuare l’opera . Come molti altri illuministi ed enciclopedisti, D’Alembert fu massone, membro della Loggia delle “Nove Sorelle” di Parigi. Per l’ Enciclopedie vedi NOTA dopo Diderot. 

George Jacques  DANTON (1759-1794)

Vincenzo DE FILIPPIS (1749-1799) matematico, filosofo e patriota italiano, considerato un martire della Repubblica Napoletana del 1799. Nella città partenopea ebbe modo di frequentare gli ambienti illuministici entrando in contatto fra gli altri con la poetessa Eleonora Pimentel Fonseca e il giurista Mario Pagano. Studiò matematica e filosofia presso il collegio Ancarano dell’Università di Bologna, discepolo del matematico Sebastiano Canterzani (1734-1818). Nel 1787 ottenne la cattedra di matematica al Real Collegio di Catanzaro ed ebbe, fra i suoi discepoli, Giuseppe Poerioː tuttavia, le cattive condizioni di salute lo spinsero ad abbandonare l’insegnamento nel 1793. Nel 1799 fu fra i principali artefici della Repubblica Napoletanaː infatti il 25 febbraio 1799, con la nomina di Ignazio Ciaia, alla guida della Repubblica napoletana in sostituzione di Carlo Lauberg, Vincenzo De Filippis entrò nel governo come ministro degli Interni. Con la caduta della Repubblica, venne messo a morte per impiccagione in Piazza Mercato (28 novembre 1799) assieme ad altri sette patrioti.

Pietro DE MARTINO (1707-1746) astronomo a Napoli, scrisse “Nuove istituzioni di aritmetica pratica”.

Denis DIDEROT (1713-1784) – 71. Fu  filosofo, enciclopedista, scrittore e critico d’arte francese. Fu uno dei massimi rappresentanti dell’Illuminismo e uno degli intellettuali più rappresentativi del XVIII secolo, amico e collaboratore di Voltaire. Fu promotore, direttore editoriale ed editore dell’Encyclopédie, con la collaborazione di d’Alembert, che  alle prime difficoltà  si ritirerà. Diderot, diresse l’opera, scrivendo circa 1500 voci, spesso anonime, e porterà avanti, dopo l’abbadono di d’Alambert, quasi da solo  l’intera impresa. Oltre al colossale lavoro enciclopedico  Diderot scrisse numerose opere filosofiche e teatrali, romanzi, articoli e saggi su disparati argomenti, occupandosi di arte, storia, politica e società. E’ importante osservare che l’opera dei “Filosofi” diventa collegiale con la stesura dell’Encyclopédie, i cui primi volumi furono dati alle stampe nel 1751. L’opera, in apparenza scientifica, fu il grande  veicolo delle nuove idee. Lo storico massone Eugene Lennhoff afferma: “Cominciò la battaglia per l’Encyclopédie, una delle più grandi opere di tutti i tempi. A capo di questa campagna fu il Massone Diderot” assieme a tutto il ‘Gotha’ dell’enciclopedismo francese, da Condorcet a Lalande, da Maine de Biran a Diderot ed Helvetius” oltre a Voltaire, che era stato iniziato alla conoscenza della luce massonica:.

NOTA. L’Encyclopédie, con i suoi 28 volumi in folio, le 71.818 voci e le 2.885 tavole, rimane comunque l’opera manifesto della età dei Lumi, oltre che il più autorevole capolavoro che illustra non solo il processo scientifico ma anche quello tecnologico, mai così celebrato prima, anche se da allora fu interpretato come simbolo concreto dell’emancipazione e del progresso umano, atto a a favorire la nascita di una moderna società civile dell’occidente. Oggi forse i fondamenti, di quella nuova filosofia illuminista che pose un legame tra il progresso umano e l’avvento di nuove tecnologie, sono messi in discussione per via di una esponenziale crescita tecnologica  che potrebbe porre il futuro dell’uomo in direzioni incerte dal punto di vista evoluzionistico. Tuttavia, ai nostri occhi moderni,  va data ancora grande  importanza  a quella che fu la scoperta dei diritti dell’uomo, alla loro costituzionalizzazione, sostanzialmente prodotta dalla creazione  della democrazia rappresentativa che nacque con  la rivoluzione americana del 1776, delle colonie che vollero la loro indipendenza con quello che fu un attacco frontale ai fondamenti dell’Antico Regime.

Giuseppe DOVERI (1792-1857) 

Leonhard EULER  (1707-1783) (minischeda)

Giovanni Francesco  FAGNANO, Marchese de’ Toschi (1715-1797), figlio di Giulio Carlo F. (1682-1766) anche lui matematico, entrambi di origine marchi-giana.  Giovanni era uno dei 12 figli della sua famiglia, ma l’unico che seguì l’interesse del padre per la matematica. Entrato in chiesa, essendo stato ordinato sacerdote, e poi nominato canonico della cattedrale di Sinigaglia nel 1752 e nel 1755 fu nominato arciprete, un alto e ambito grado per quei tempi. Presentò un teorema sui triangoli : le altezze di un triangolo acutangolo sono le bisettrici del suo triangolo ortico, dunque l’ortocentro del primo è l’incentro del secondo. In realtà questo teorema può essere visto come la conseguenza di un famoso problema detto problema di Fagnano: “come si devono scegliere tre punti P, Q, R sui tre lati di un triangolo acutangolo ABC affinché sia minimo il perimetro del triangolo PQR?”. Nel suo studio sulla rettificazione della lemniscata, Fagnano ha introdotto trasformazioni analitiche ingegnose che hanno gettato la base per la teoria degli integrali ellittici ed il suo lavoro ha contribuito alla introduzione delle funzioni ellittiche. 

Nicola FERGOLA (1753-1824) fece studi umanistici e giuridici; dopo una laurea in legge, studiò matematica con Giuseppe Marzucco (1713—1800), di cui fu successore nella cattedra all’Università di Napoli nel 1800. attorno al 1771 Fergola abbia aperto una scuola privata a Napoli; nello stesso periodo fu nominato professore al “Liceo del Salvatore“, un istituto regio fondato nel 1770 in luogo di un collegio della Compagnia di Gesù, soppressa da Papa Clemente XIV nel 1769. Al Liceo del Salvatore per molti anni Fergola fu professore di Filosofia; ottenne la cattedra di Matematica analitica e di fisica matematica, con obbligato alla pubblicazione delle lezioni, solo alla fine del 1789. Alcune delle opere più interessanti, per esempio le Prelezioni sui Principi matematici della filosofia naturale del cavaliere Isacco Newton (1792–93), sono nate come dispense delle lezioni. Al Liceo del Salvatore Fergola ebbe numerosi allievi: Felice Giannattasio, Carlo Forti, Pietro Schioppa, Francesco Bruno, Luigi Telesio (che divenne biografo di Fergola^[1]), Vincenzo Flauti, Giuseppe Battaglini, Giuseppe Scorza e soprattutto Annibale Giordano il quale giovanissimo, nel 1787, pubblicò una generalizzazione del “problema di Pappo” (o di Castillon).

Nicola FIORENTINO (1755-1799)

Vincenzo FLAUTI (1782-1863) allievo di Fergola. MATEMATICI NAPOLETANI DEL 1700 (vai a) ancora(vai a profilo Vincenzo Flauti).

Gregorio FONTANA (1735-1803) nato nel Trentino, fratello del fisico Felice Fontana (1730–1805), vedi FISICA !700-1800.. Membro degli scolopi, essendosi distinto negli studi di MATEMATICA succedette a Ruggero Giuseppe Boscovich (1711-1787) nella cattedra di matematica a Pavia, dove proseguì gli studi sull’analisi e fu direttore della biblioteca Universitaria. Il 16 aprile 1795 divenne membro della Royal Society. MASSONE, come il fratello Felice,  fece parte della Loggia milanese affiliata alla Gran Loggia Provinciale della Lombardia, dipendente dalla Gran Loggia Nazionale di Vienna.

Vittorio FOSSOMBRONI ( 1754 –  1844) è stato un matematico, ingegnere, economista, politico e intellettuale italiano. Fu 1° ministro del Granducati di Toscana.

Joseph FOURIER (1768-1830) – 62. Noto per le serie e la trasformata di Fourier.

 

 

 

Paolo FRISI (1728-1784)

 

 

 

Paolo Frisiani (797 –  1880) è stato un astronomo e matematico milanese.  Si formò come astronomo frequentando l’Osservatorio astronomico di Brera dove, nel 1834, divenne secondo astronomo.

Thomas FULLER (1710-1790)

 

 

 

 

Karl Friederich Johann GAUSS (1777-1855)(minischeda)

 

 

 

Joseph Diez GERGONNE (1771-1859)

Sophie GERMAIN (1776-1831) (vai a)  è stata una matematica francese. È nota per il suo lavoro sulla teoria dei numeri e per aver dimostrato il teorema di Fermat sulle curve ellittiche. Germain ha anche contribuito allo sviluppo della teoria dei numeri primi e della teoria dei numeri complessi.

 

Felice GIANNATTASIO (1759-1849) sacerdote, amico e collaboratore di Nicola Fergola. Occupò la cattedra di mateatica al Collegio militare di Napoli e quella di Astronomia e di Sintesi sublime all’Università di cui fu pure rettore. Prima della rivoluzione pubblicò Riflessioni sulla quadratura dell’iperbole e un Trattato sulle Sezioni coniche (1791) e dei libri a servizio della sua scuola: Opuscoli di nostra scuola e Tactionum per la soluzione di problemi. Contribuì alla pubblicazione delle opere del matematico Michele Forte seguendo una via diversa da quella percorsa da Antonio Fontana, quella dell’Analisi elementare. Aveva quaranta anni quando Napoli visse l’esperienza rivoluzionaria, durante la quale subì i danni del sospetto e dell’isolamento vedendo anche la chiusura della sua scuola. Ebbe i maggiori impegni nel periodo napoleonico quando fu professore al Liceo del Salvatore (1806) ed ebbe la cattedra di “Astronomia e di Sintesi sublime” (1812) e quella di “Meccanica celeste”

Annibale GIORDANO (1769-1835).  MASSONE. Da adolescente Annibale Giordano frequentò la scuola di Nicolò Fergola, e nel 1789, l’anno della Rivoluzione francese, divenne professore nell’Accademia militare della Nunziatella, diventando così collega del chimico Carlo Lauberg (1762-1834), MASSONE. Nel 1790 Giordano e Lauberg aprirono a Napoli una Accademia di chimica e matematica, che divenne un centro di raccolta per i progressisti e i MASSONI napoletani; fra i frequentatori vi erano Mario Pagano, Emanuele De Deo, Francesco Lomonaco e il matematico  Vincenzo De Filippis. Nel 1792 Giordano e Lauberg scrissero i Principi analitici delle Matematiche, nella quale teorizzarono l’impegno politico dei matematici; questo saggio fu l’ultima opera scientifica di Annibale Giordano. Annibale Giordano partecipò attivamente alla vita dell’effimera Repubblica Napoletana (1799) come addetto al comitato militare e poi capo della contabilità della Marina. Caduta la Repubblica (giugno 1799), fu di nuovo imprigionato dai Borbonici nel Castel Nuovo con altri diciotto tra cui Mario Pagano, Domenico Cirillo e Giuseppe Leonardo Albanese. Il 27 gennaio 1800 fu condannato a morte dalla giunta; ma la condanna fu commutata in prigionia nell’isola di Favignana, da dove uscì con gli altri detenuti politici nel luglio 1801 grazie al trattato di Lunéville. La mancata esecuzione venne spiegata da molti come il compenso per la delazione di Giordano^[5]; altri la attribuirono a interventi a suo favore da parte del padre o del Fergola presso la corte borbonica^[8]. Giordano si rifugiò in Francia dove fu assunto in qualità di geometra del catasto del Dipartimento dell’Aube; nel 1824 fu naturalizzato francese e assunse il cognome Jourdan.

HEILBRONNER J.G. (1742 – ??) storico della matematica

Paul HENRI (1723-1789)

Johann Friedrich HERBART (1776-1841) filosofo degli iperspazi

William George HORNER (1786-1837) fu educato alla Kingswood School di Bristol. All’età di soli 14 anni divenne assistente professore nel 1800 e professore quattro anni più tardi. Noto per la regola di Horner per risolvere un’equazione algebrica che Augustus De Morgan e altri gli attribuirono, e che pubblicò nel 1830. Fuller scoprì che Theophilus Holdred, un orologiaio inglese, pubblicò il metodo in un articolo del 1820, e paragonò il plagio di Horner ad un vero e proprio ladrocinio. Questa discussione è alquanto discutibile dal momento che il metodo fu anticipato nel XIX secolo in Europa da Paolo Ruffini (per il quale vinse la medaglia d’oro attribuita a chi avesse migliorato le soluzioni numeriche delle equazioni dalla Società Italiana per le Scienze Matematiche), ma è stato, in ogni caso, considerato da Zhu Shijie in Cina nel XIII secolo.

William HIGGINS  (? 1752  – 1825)

HINDEBURG C.F. (???-???) scrive con J. Bernoulli

 

Simon Antoine L’HUILIER (1750-1840), nato a Ginevra, che viveva nella città polacca di Pulawy,  dove faceva il tutore del figlio del principe Adam Kazimierz Czartorysky, che fu per primo ministro dell’educazione in Europa. La sua fama è legata alla vincita di un premio dell’Accademia di Berli-no. Notizie e riassunto tratti da: Loredana Biacino (2024). Il problema dell’infinito e l’Exposition élémentaire desprincipes des calculs supérieurs di Simon A. L’Huilier, Periodico di Matematica, Anno 39°(s.IV)_Vol. VI_ (1)_63-120. (Vai a riassunto).

 KLUGEL G.S. (1739-1812)

Joseph-Louis LAGRANGE  (1736-1813)

(vai a)

 

 

 

Johann Heinrich LAMBERT (1728-1777), filosofo, matematico, fisico e astronomo svizzero, contemporaneo di Eulero. Fu un pioniere della geometria non euclidea. Provò nel 1761,  che π essendo eguale ad arctang 1, è un numero irrazionale (provò molto di più, precisamente che  l’arcotangente di un qualsiasi numero razionale è irrazionale). Provò  provò che se  x è un razionale non nullo, allora tan⁡g x è irrazionale. Da tang (π/4) = 1, segue l’asserto. Nel campo della fisica lasciò importanti contributi in fotometria. Nel campo dell’astronomia risolse il problema della determinazione di un’orbita nello spazio, noto come problema di Lambert.

Gabriel LAME’ (1795-1870)

J.J. Lefrançois de LALANDE (1732-1807).

Pierre-Simon LAPLACE (1749-1827) (minischeda)

Antoine-Laurent LAVOISIER (1743-1794)

Adrien-Marie LEGENDRE (1752-1833)

 

 

 

 

Enoch LEWIS (1776-1856). Fu uno dei primi matematici del nuovo mondo. Dal 1795 come geometra lavorò per la creazione di città della Pennsylvania occidentale. Apparteneva alla Society of Friends (Quaccheri), insegnò nel Dipartimento di matematica di William Penn Charter School (Accademia degli amici) a Filadelfia, nel 1796-1799, in seguito fu insegnante di matematica presso il Westtown School, Pennsylvania, e nel 1808 aprì una scuola privata per studenti di matematica a New Garden Township, Contea di Chester, Pennsylvania, che ha insegnato con successo per diversi anni. Campi di studio la  Geometria e in particolare le sezioni coniche, esperto di educazione matematica.  (per saperne di più).

Simone- Antoine-Jean  L’HUILIER (1750-1840) si è occupato di Teoria dei grafi.  Vedi HUILIER

Nikola Ivanovic LOBACEWSKI (1793-1856)

John MACHIN (1680 – 1751) è stato un matematico e astronomo inglese. Nel 1706 sviluppa una formula, rapidamente convergente, per il calcolo di pi greco, con la quale calcolò pi con 100 cifre decimali :  π/4 = 4 arctang (1/5) – arctang (1/239). Questa, ed altre formule da essa derivate, furono la base per il calcolo di pi greco fino all’avvento del computer. Machin fu segretario della Royal Society dal 1718 al 1747, e professore di astronomia al Gresham College di Londra dal 1713. Fece parte della Commissione che nel 1712 esaminò la disputa Leibniz-Newton. Nel 1728 fu elencato come uno dei contributori alla Cyclopaedia di Chambers.

Gianfranco MALFATTI (1731-1807). Risolse il problema di iscrivere in un triangolo dato tre circonferenze, tra loro tangenti, ognuna delle quali tocchi due lati del triangolo. Si occupò anche di teoria delle equazioni algebriche. La Risolvente di Malfatti è una equazione di 6º grado, calcolando una radice della quale si può risolvere completamente l’equazione generale del 5º grado, peraltro non  risolubile per  radicali, a norma del teorema di Ruffini-Abel.

Giuseppe MARZUCCO (1713—1800), professore di Nicola Fergola, occupò una cattedra  all’Università di Napoli nel 1800 sulla quale nel 1800 successe il Fergola.

Lorenzo MASCHERONI (1750-1800) (vai a)

Ottaviano Fabrizio MOSSOTTI (1791-1863)

 

Nel 1840, nel quadro del rilancio dell’attività scientifica dell’ateneo voluto dal governo granducale, Mossotti fu poi chiamato a Pisa per insegnare Fisica matematica e Meccanica celeste. Qui, dove ebbe tra gli allievi Enrico Betti, fu tra i fondatori della scuola matematica pisana. Nel 1848 partecipò alla battaglia di Curtatone e Montanara come comandante del Battaglione universitario pisano.

Francesco Domenico MICHELOTTI (1710-1787)

August Ferdinand MOBIUS (1790-1868)

Gaspard MONGE (1746-1818) (minischeda)

 

 

Jean-Etienne  MONTUCLA (1725- ). Nel 1754 pubblicò un trattato anonimo intitolato Histoire des recherches sur la quadratura du cercle, e nel 1758 terminò la prima parte della sua grande opera, Histoire des mathématiques (Storia delle matematiche), il primo vero studio storico di questa disciplina, riprendendo un precedente progetto di Pierre de Montmort (1678-1719). Fu nominato intendente-segretario di Grenoble nel 1758, segretario della spedizione per la colonizzazione di Cayenne nel 1764, e capo architetto e censore reale per libri di matematica nel 1765. A Parigi fu anche collaboratore per la Gazette de France. Nel 1778 ripubblicò Recreations mathématiques di Jacques Ozanam, poi pubblicato in inglese da Charles Hutton (4 volumi, Londra, 1803).

 

Ambrogio MULTEDO (1753-1840) -87  Abate e matematico

Niccolò PAGANINI (1782-1840). Le proporzioni relative alla sezione aurea e al collegamento con i numeri di Fibonacci si ritrovano anche in musica: da Paganini a Bach, fino a Mozart, Beethoven e Stravinskij. Nel XVIII secolo si costituì persino una società di scienze musicali con lo scopo di mostrare i legami tra musica e matematica, alla quale aderirono musicisti come Bach e Händel. E ancora oggi la serie di Fibonacci torna a far parlare di sé: i Genesis l’hanno ripetutamente evocata nella costruzione armonico-temporale dei loro brani, così come i Deep Purple nel brano Child in Time e i Dream Theater nell’album Octavarium, interamente concepito secondo il rapporto tra i numeri 8 – 5 e i termini consecutivi della sequenza di Fibonacci. Uno studio originale sulla rilevazione dei rapporti matematici – in primo luogo della sezione aurea – nelle opere del celebre violinista e compositore Niccolò Paganini svela lo strettissimo rapporto tra musica e matematica. L’incontro si propone di esporre i risultati della ricerca, analizzando i criteri formali della composizione musicale e i suoi cambiamenti nell’opera paganiniana. I principi teorici evidenziati saranno narrati in musica, attraverso brevi esecuzioni dal vivo per violino solo.

• La seconda coppia più piccola di numeri amicabili (1.184 e 1.210) fu identificata solo nel 1867 da un ragazzo di 16 anni, Niccolò Paganini, omonimo del celebre violinista!

Pietro PAOLI (1759-1839) matematico, fisico e astronomo.  studiò presso i gesuiti di Livorno,  dal 1774 frequentò l’Università di Pisa per giurisprudenza, ma si spostò  sulle scienze fisiche e matematiche. Si  laureò nel 1778. Insegnò al ginnasio di Mantova, nel 1782 fu chiamato a ricoprire la cattedra di Matematiche elementari presso l’Università di Pavia.per passare poi all’Università di Pisa. Si occupò di geometria analitica, analisi, equazioni differenziali ordinarie e parziali. Nei suoi lavori Paoli dimostra di possedere una profonda e completa conoscenza delle opere di Lagrange, Laplace e Monge.

Gioacchino PESSUTI (1743-1814), collabora con Vincenzo Riccati.

Francesco PEZZI (17864-1816) – 62 Ingegnere militare, professore di matematica e ingegneria militare, da non confondere con l’omonimo giornalista nato 1780.

 

 

Gabrio PIOLA Daverio (1794-1850) matematico e fisico

Antonio PINAZZO (1750-1849) – 99  gesuita matematico

Giovanni Amedeo PLANA (1781-1864), matematico e Astronomo

 

 

 

John PLAYFAIR (1748-1819)   matematico e filosofo scozzese. Noto per il suo libro Illustrations of the Huttonian Theory of the Earth – Illustrazioni della teoria huttoniana della Terra, (1802), scritto con l’unico obiettivo di chiarire ciò che James Hutton aveva già dimostrato. È stato attraverso questo libro che il principio di Hutton di uniformitarismo, successivamente ripreso da Charles Lyell, ha raggiunto il vasto pubblico. Il libro di testo di Playfair Elementi di Geometria è famoso, specialmente nella letteratura  per la riformulazione dell’assioma euclideo relativo alle parallele noto ora come assioma di Playfair (1795).  Fu segretario generale della Royal Society di Edimburgo.

Louis  POINSOT (1777-1859) si è occupato di Teoria dei grafi.

Simon-Denis POISSON (1781-1840)-59

 

 

 

Jean-Victor PONCELET (1788-1867). Studia le sezioni coniche e sviluppa il principio di dualità. E’ professore di meccanica alla école d’application nel 1825. Nelle sue lezioni studia lo stato di materiali sottoposti a sollecitazioni. Si interessa  alla progettazione di turbine e ruote idrauliche, e disegna una turbina Francis nel 1826 ( costruito nel 1838). Nel suo libro “Meccanica industriale” (1829) studia il lavoro e l’energia cinetica. Alcuni gli attribuiscono la definizione del lavoro come prodotto di forza e traslazione. Nel 1835 e diventa professore di meccanica alla Sorbona nel 1838. Dal 1848, comanda la École Polytechnique con il grado di generale. Si ritira quindi nel 1850 per dedicarsi alla ricerca matematica..

 

 

 

Jacopo Francesco RICCATI (1676-1754), matematico trevigiano, padre di Vincenzo e giordano anch’essi matematici.Noto per lo studio dell’equazione differenziale  y’ = a(x) + b(x) y + c(x) y² che porta il suo nome, equazione che, al contrario delle equazioni differenziali lineari, non sono generalmente risolvibili in modo elementare.

 

Giordano RICCATI (    ) è stato un matematico e fisico italiano. Primogenito di Jacopo Riccati e fratello di Vincenzo, 

Vincenzo RICCATI (1707 – 1775) è stato un matematico e fisico italiano. Secondogenito di Jacopo Riccati, e fratello di Giordano. Le sue ricerche principali continuarono quelle del padre nell’analisi matematica, specialmente nel campo delle equazioni differenziali, e nella fisica. Da lui prendono il nome le equazioni di Riccati, alcuni tipi di equazioni differenziali. Negli anni dal 1749 al 1753, ebbe contatti anche con i  matematici italiani: Gioacchino Pessuti (1743-1814), Leonardo Ximenes (1716-1786), Gaetana Maria Agnesi e Tommaso Maria Gabrini I726-1808). Un suo alunno fu Girolamo Saladini (1735-1813), con il quale scrisse le Institutiones Analyticae, in tre volumi pubblicati a Bologna nel 1765–67, presso la Stamperia di San Tommaso d’Aquino

Paolo RUFFINI  (1765-1822) (vai a)

 

Teorema di Ruffini- Abel

 

William Rutherford (1798 – 1871) matematico inglese  noto per aver calcolato nel 1841 ben 208 cifre di phi greco (di cui 152 corrette), superando il record precedente di Jurij Vega (1754-1802), che nel 1759 diede 126 cifre corrette. Per i calcoli usò la formula:    phi/4 =4arctan⁡(1/5)−arctan⁡(1/70)+arctan⁡(1/99), derivata dalla formula di Machin.

 

Adhémar-Jean-Claude Barré de SAINT-VENANT ( 1797 –  1886) è stato un matematico e ingegnere francese. Ottenne i più significativi risultati nello studio della resistenza dei materiali e della teoria dell’elasticità, di cui è considerato uno dei fondatori. Trave di Saint- Venant e Principio di Saint-Venant. 

Girolamo SALADINI (1735-1813)  un matematico italiano, operante a Bologna. Fu un brillante allievo del matematico Vincenzo Riccati, col quale ebbe una collaborazione feconda: insieme scrissero le Institutiones Analyticae, in tre volumi pubblicati a Bologna nel 1765–67 . In una sua memoria del 1808, intitolata Sul principio delle velocità virtuali, rifacendosi a Vittorio Fossombroni e a Vincenzo Angiulli, cercò di dimostrare il principio delle velocità virtuali, eludendo le difficoltà principali, tra cui quelle dovute alla presenza dei vincoli.

 

Heinrich Christian SCHUMACHER (1780-1850)

Ferdinand Karl SCHWEIKART (1780-1857)  suelle parallele

 

Mary SOMMERVIL:LE (1780 -1872) è stata una matematica, astronoma e scrittrice scozzese. È stata la prima donna a ricevere una laurea honoris causa in matematica dall’Università di Oxford. Somerville ha contribuito in modo significativo allo sviluppo dell’astronomia e della fisica matematica. È nota per i suoi libri divulgativi sulla scienza, tra cui On the Connexion of the Physical Sciences (1834).. 

Karl George Christian  Von STAUDT (1797-1867)

Jakob STEINER (1796-1863) Teorema di Steiner sulla generazione proiettiva delle coniche: Ogni conica è il luogo delle intersezioni di rette di due fasci, che si corrispondono in una proiettività. Viceversa se da due punti distinti di una conica proiettiamo i punti della conica otteniamo due fasci che sono corrispondenti in una proiettività. Si veda lo studio del Deltoide tricuspidale  o ipocicloide e la in ellisse di Steiner. 

Placido TARDY (Messina, 23 ottobre 1816 – Firenze, 2 novembre 1914) è stato un mate-matico e fisico italiano. Fu professore di matematica all’Università di Messina dal 1841 al 1847, quando lasciò il Regno delle Due Sicilie per le sue posizioni pro-risorgimentali, dopo i tumulti violenti che scoppiarono nel settembre di quell’anno a Reggio Calabria e Messina. Si rifugiò prima a Firenze e nel 1850 a Genova. Nella città ligure insegnò per un anno matematica al Liceo cittadino e, successivamente, geometria e calcolo infinitesimale alla Scuola di Marina e, dal 1859, all’Università di Genova, della quale fu Rettore per 6 anni in diversi periodi: dal 1º novembre 1865 al 31 ottobre 1868 e dal 1º novembre 1878 al 31 ottobre 1881.

Adolph TAURINUS (1794-1874) nipote di SCHWEIKART (1780)

Bernhard Friederich THIBAUT (1775-1832)

Giuseppe TORELLI (1721-1781)

 

 

 

 

Alexandre-Theophile VANDERMONDE (1735-1796)-62

si è occupato di Teoria dei grafi.

 

 

yyy

Jurij Bartolomej VEGA  (1754-1802) matematico ingegnere navale sloveno  che nel 1789 trovò 140 cifre di phi greco,  di cui solo le prime 126 erano corrette. Migliorò Machin che aveva calcolato phi con 100 cifre usando un miglioramento della  formula di  Machin : π/4 = 5 arctang (1/7) – 2arctang (3/79). Mantenne il record mondiale per 52 anni, fino al 1841, quando il primato fu migliorato da William Rutherford (1798 – 1871) che diede 152 cifre corrette. Nel 1780 lasciò Lubiana per prestare il servizio militare a Vienna, dove fu nominato professore di matematica alla Scuola di Artiglieria. Militare muore in battaglia. Nel 1796 gli fu conferito dal governo asburgico l’Ordine di Maria Teresa. Nel 1800 gli fu attribuito il titolo ereditario di Barone.La Slovenia ha emesso una banconota da 50 Tolar che lo rappresenta. L’asteroide 14966 Jurijvega, scoperto nel 1997, porta il suo nome.

Alessandro Volta (1745-1827). fisico a Pavia.

Friedrich Ludwig WACHETER (1792-1817),allievo di Gauss, e professore di matematica al ginnasio di Danzica, aveva chiamato geometria anti-euclidea le  geom. non euclidee

William WALLACE (1768-1843) è stato un matematico e astronomo scozzese, inventore del pantografo.

Edward WARING (1736-1798), matematico inglese. A partire dal 1760 fino alla sua morte, insegnò matematica all’Università di Cambridge col titolo di Professore Lucasiano. Si trattava del più antico titolo per l’insegnamento della matematica a Cambridge, associato alla Lucasian Chair of Mathematics. Fu  ben noto per la formulazione del cosiddetto “problema di Waring” proposto nel 1770, nelle forma seguente: esiste per ogni numero naturale k, un intero positivo m tale che ogni numero naturale sia la somma di al più m potenze k-esime di numeri naturali? La risposta affermativa, nota come Teorema di Hilbert-Waring, fu fornita da David Hilbert nel 1909.

 

Caspar WESSEL (1745-1818)

 

John WILSON (1741-1793), matematico inglese allievo di Waring. Enunciò il famoso Teorema che porta il suo nome : n è primo se e solo se n!+1 è congruo a zero mod n.  Il teorema di Wilson era noto ad Ibn al-Haytham (965-1040), uno dei più importanti e geniali scienziati del mondo islamico. Fu annunciata da  Edward Waring nel 1770, come scoperta di Wilson, ma priva di dimostrazione. Il teorema fu provato per la prima volta da Joseph-Louis Lagrange (1736-1813), l’anno dopo, nel 1771.

Josef Maria Hoene Wroski (1778- 1853) .Dal 1794 al ’98 servì l’esercito russo ottenendo il grado di tenente colonnello. A partire dal 1800, quando si trasferì nella legione polacca a Marsiglia, cominciò a interessarsi di Filosofia e Scienza. Wronski concepì una riforma della Filosofia, della Matematica, dell’Astronomia e della Tecnica come fondamento di una riforma dell’intero sapere umano.  Nel 1803 entrò all’Osservatorio di Marsiglia e qui sviluppò una teoria sulla struttura e origine dell’Universo. Nel ’10 pubblicò un volume sui fondamenti della Matematica: le sue teorie si rifacevano a Pitagora e al concetto di numero come entità essenziale dell’Universo. Nel 1812 pubblicò poi un articolo (Résolution générale des équations de tous degrés) in ogni caso errato.

Chiamasi wroskiano di n funzioni, di una varibile reale, il determinante della matrice quadrata costruita mettendo le funzioni nella prima riga, la derivata prima di ogni funzione nella seconda riga, e così fino alla derivata n-1. 

Leonardo XIMENES (1716-1786), collabora con Vincenzo Riccati.