EUCLIDE (IV-III sec. a.C.)

Euclide (323-283 a.C. (a 40 anni)) – scheda su Euclide

F. Enriques (1932). Elementi di Euclide-Libro X (1932)

F. Enriques (1935). Elementi di Euclide-Libri XI-XIII (1935)

F.Eugeni (2020). Gli assiomi della geometria euclidea secondo Hilbert e Moore

PROFILO

Euclide è menzionato in un brano di Pappo, ma la testimonianza più importante su cui si basa la storiografia che lo riguarda viene da Proclo, che lo colloca tra i più giovani discepoli di Platone.

«Non molto più giovane di loro, Ermotimo di Colofone e Filippo di Mende, Euclide; egli raccolse gli “Elementi”, ne ordinò in sistema molti di Eudosso, ne perfezionò molti di Teeteto, e ridusse a dimostrazioni inconfutabili quelli che suoi predecessori avevano poco rigorosamente dimostrato. Visse al tempo del primo Tolomeo, perché Archimede, che visse subito dopo Tolomeo primo, cita Euclide; e anche si racconta che Tolomeo gli chiese una volta se non ci fosse una via più breve degli Elementi per apprendere la geometria; ed egli rispose che per la geometria non esistevano vie fatte per i re. Euclide era dunque più giovane dei discepoli di Platone, ma più anziano di Eratostene e di Archimede che erano fra loro contemporanei, come afferma in qualche luogo Eratostene. Per le idee Euclide era platonico e aveva molto familiare questa filosofia, tanto che si propose come scopo finale di tutta la raccolta degli Elementi la costruzione delle figure chiamate platoniche»

(Proclo, Commento a Euclide, II, 68)

Sul finire del IV secolo a.C., Tolomeo I, allora faraone, sovrano illuminato, puntiglioso e propositivo nei suoi sforzi governativi, istituì ad Alessandria una scuola, chiamata Museo. Chi insegnava in questa scuola era un gruppo di studiosi, tra cui Euclide.

Euclide fu uno degli iniziatori dell’assettamento assiomatico delle teorie matematiche, impegno che venne intrapreso a partire dal suo secolo e che prevede assiomi e teoremi, che sono conseguenza dei primi.

Mentre oggi le parole di assioma e postulato sono dei sinonimi, Euclide nei suoi Elementi individua cinque assiomi che riguardano nozioni comuni e cinque postulati che riguardano la geometria. Gli assiomi sono proprietà che non devono essere dimostrate, essi esprimono le relazioni esistenti fra gli enti primitivi. Sembra che lo stesso Euclide non fossedel suo V postulato, ovvero della sua versione dell’assioma delle parallele, perché non vi fece ricorso se non dopo aver dimostrato tutti i teoremi che si potevano provare senza di esso. I postulati di Euclide sono cinque, di cui i primi quattro immediatamente evidenti e verificabili sul modwllo fisico-intitivo. Essi sono:

Tra due punti qualsiasi è possibile tracciare una e una sola retta;
Si può prolungare una retta oltre i due punti indefinitamente;
Dato un punto e una lunghezza, è possibile descrivere un cerchio;
Tutti gli angoli retti sono uguali.

Il quinto, quello delle parallele, risulta essere non evidente e separato dagli altri quattro:

se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, prolungando indefinitamente le due rette, esse si incontreranno dalla parte dove la somma dei due angoli è minore di due angoli retti o come è più comunemente definito secondo l’assioma di Playfair: data una qualsiasi retta r ed un punto P non appartenente ad essa, è possibile tracciare per P una ed una sola retta parallela alla retta r data.

La particolare formulazione dell’assioma da parte di Euclide era un modo per evitare l’affermazione esplicita che esistono coppie di rette infinite perché, se fossero state finite, non avrebbero potuto essere prolungate tanto quanto fosse stato necessario in ogni contesto, considerato che egli dimostrò l’esistenza di rette parallele.

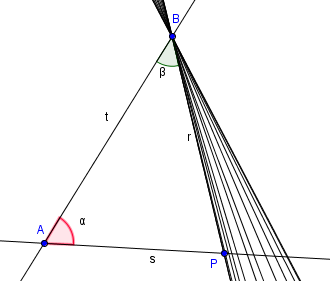
Prendendo in esame questa figura, se si mantengono fisse t ed s e si fa ruotare r in senso antiorario intorno a B, secondo il V postulato r continuerà ad incontrare s finché a+b<180. Possiamo però notare che, al ruotare di r, il punto P si allontana sempre di più da A su s, finendo per uscire dallo schermo e non essere più osservabile. Quindi non è possibile verificare che la retta r non abbia più un punto in comune con s quando a+b=180. Questa proposizione risulta falsa in un universo di dimensioni finite. Immaginiamo infatti che il piano contenente r e P sia limitato alla zona interna ad un cerchio, si vede immediatamente che vi sono molte rette passanti per P che non incontrano r.

GLI ELEMENTI

Nel primo libro degli “Elementi”, Euclide introduce gli oggetti geometrici fondamentali (e cioè il piano, la retta, il punto e l’angolo); dopodiché, egli tratta le proprietà fondamentali dei cerchi e dei poligoni, enunciando anche il teorema di Pitagora.

Nel Libro V si parla della teoria delle proporzioni, mentre nel Libro VI tale teoria viene applicata ai poligoni. I Libri VII, VIII e IX affrontano i concetti di numeri perfetti, numeri primi, massimo comun divisore e altre questioni di aritmetica, mentre il Libro X è incentrato sulle grandezze incommensurabili. Infine, i Libri XI, XII e XIII parlano di geometria solida, affrontando lo studio di piramidi, sfere, cilindri, coni, tetraedri, ottaedri, cubi, dodecaedri e icosaedri.

Gli “Elementi” non costituiscono un riassunto delle conoscenze matematiche dell’epoca, ma una sorta di manuale introduttivo che riguarda l’intera matematica elementare: l’algebra, la geometria sintetica (dei cerchi, dei piani, delle linee, dei punti e delle sfere) e l’aritmetica (la teoria dei numeri).

Negli “Elementi” vengono enunciati e dimostrati 465 Teoremi (o Proposizioni), ai quali si aggiungono i corollari e i lemmi (quelli che oggi sono conosciuti come primo e secondo teorema di Euclide in realtà sono corollari dalla Proposizione 8 contenuta nel Libro VI).

Euclide nella propria vita scrisse diverse altre opere. Queste parlano di ottica, di sezioni coniche, di altri argomenti di geometria, di astronomia, di musica e di statica. Molte di esse sono andate perdute, ma quelle che si sono conservate (e soprattutto la “Catottrica”, che parla di specchi, e l'”Ottica”, che parla di visione) hanno esercitato un’influenza molto importante sulla matematica, sia per gli arabi che durante il Rinascimento. Tra le altre opere, si ricordano l'”Introduzione armonica” (un trattato di musica), i “Luoghi superficiali” (andato perso), la “Sezione del canone” (un altro trattato di musica), le “Coniche” (a sua volta andato perso), i “Fenomeni” (una descrizione della sfera celeste), i “Dati” (connessi con i primi sei libri degli “Elementi”) e i tre libri dei “Porismi” (tramandati sino a noi solo attraverso il riassunto realizzato da Pappo di Alessandria).