torna a matematici dell’antichità
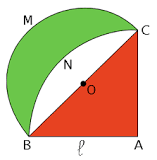
Sia dato un triangolo rettangolo isoscele ABC con cateto “l”. Facendo centro in O si tracci la semicirconferenza CMB di raggio OB e, facendo centro in A, si tracci l’arco CNB di raggio AB.
Si viene così a formare, esternamente al triangolo, una lunula, cioè una figura piana limitata da due archi di circonferenza di diverso raggio, aventi gli estremi in comune e situati dalla stessa parte di piano rispetto alla corda che coniuga tali estremi.
Si può dimostrare che la lunula (zona verde) ha la stessa area del triangolo (zona rossa) infatti: Dunque, se le aree della zona verde e della zona rossa, aumentate entrambe dell’area della zona bianca, formano due superfici tra loro equivalenti, ne consegue che la lunula e il triangolo sono anch’essi equivalenti.
Proviamo ora che appunto la lunula ha la stessa area del triangolo, infatti:
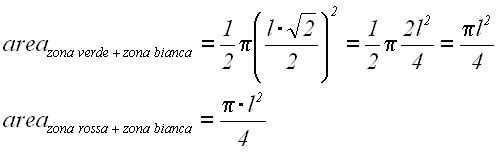
Dunque, se le aree della zona verde e della zona rossa, aumentate entrambe dell’area della zona bianca, formano due superfici tra loro equivalenti, ne consegue che la lunula e il triangolo sono anch’essi equivalenti.
Questa scoperta è dovuta ad Ippocrate di Chio e può essere considerato lo stimolo, nella storia della matematica, verso uno dei più celebri problemi: “La quadratura del cerchio”.
Il Teorema di IPPOCRATE (attribuito). Le aree di due cerchi stanno tra loro come i quadrati costruiti sui loro diametri ( o anche ovviamente come i quadrati costruiti sui raggi).