Le formule di Brahamagupta.
di Franco Eugeni
Nella sua forma tipica e più facile da ricordare, la formula di Brahmagupta afferma che l’area di un quadrilatero ciclico (ovvero iscritto in una circonferenza) i cui lati hanno lunghezze a, b, c, d è uguale a:
Nel caso di quadrilateri non ciclici, l’estensione della formula di Brahmagupta è costituita dalla formula di Bretschneider, che coinvolge anche la misura di due angoli opposti del quadrilatero:
dove la misura dell’angolo θ è la metà della somma di due angoli opposti (la scelta della coppia è irrilevante (se si considerano gli altri due angoli, la metà della loro somma è supplementare a θ; dal momento che cos ( π -θ) = – cos θ, abbiamo cos2( π -θ) =cos2 θ.
Del resto una nota proprietà dei quadrilateri ciclici è il fatto che gli angoli opposti sono supplementari. Di conseguenza, essendo in questo caso θ = π/2, risulta essere nella formula: abcd cos2 θ == abcd cos2 (π/2) = 0, riducendosi alla formula di base.
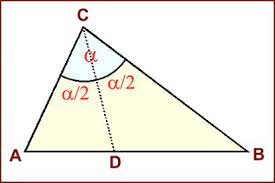Problema. Sia dato un triangolo di cui si conoscano le misure di due lati a, b e la misura α dell’angolo compreso. Si vuole trovare la misura del segmento di bisettrice CD.
Occorre ricordare che l’area A del triangolo ABC è data da: A = (1/2) ab senα.
Ma è anche posto CD = x, A = (1/2) ax sen (α/2) + (1/2) bx sen (α/2), da cui egua-gliando: CD = x = ab senα / [(a+b) sen (α/2)] (formula di Brahamagupta).